تصميم العناصر الإنشائية للجدران الاستنادية ج(2)

​

& ومن الأنواع الأخرى من الجدران الاستنادية ما يلي:

الجدران الاستنادية ذات التدعيم المعاكس: توجد طرق عديدة لحساب البلاطات الشاقولية للجدران ذات التدعيم المعاكس وإذا اعتمدنا الدقة في الحسابات فيجب اعتبار بلاطات جسم الجدار والكعب المحصور بين الدعامات كبلاطات مستمرة من ثلاث جهات وحرة من الاتجاه الرابع وهناك جداول خاصة لحساب عزوم الانعطاف المؤثرة على البلاطات. وتتلخص طريقة البروفسور هانتينغتون  بما يلي:

• تصميم بلاطة الجزع بالاتجاه الأفقي كبلاطة مستمرة ممتدة أفقيا تتعرض للدفع الجانبي للتربة الشكل رقم (4، a).

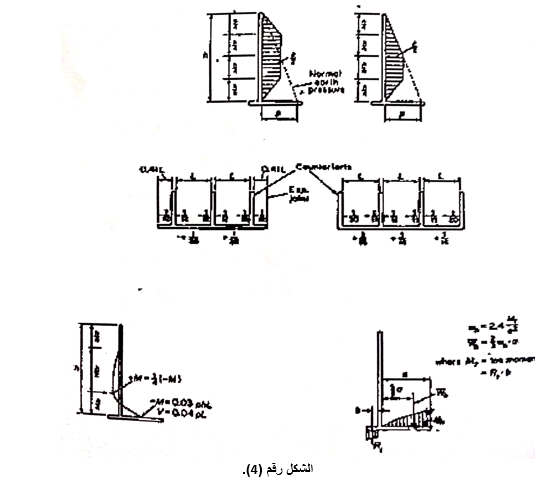
• تصميم بلاطة الجزع بالاتجاه الشاقولي كبلاطة تعمل بالاتجاه الشاقولي معرضة لعزوم انعطاف موجبة وسالبة كما هو مبين بالشكل رقم (4،b).
• تتعرض بلاطة الكعب إلى القوى المبينة في الشكل (2، d) بالإضافة إلى قوى موزعة باتجاه الأسفل تكافئ تأثير عزوم انعطاف بلاطة القدم تتوزع هذه القوة بشكل قطع مكافئ تأخذ قيمتها العظمى عند نهاية الكعب ومقدارها. W_b= 2.4 M_q/b²

حيث: M_q: عزم الانعطاف المؤثر على ١ متر طولي من بلاطة القدم.

B: طول المكعب.

وتكون محصلة هذه القوة 3/2 من W_b.a  وتؤثر على بعد 8/5 من a من ظهر الجدار.

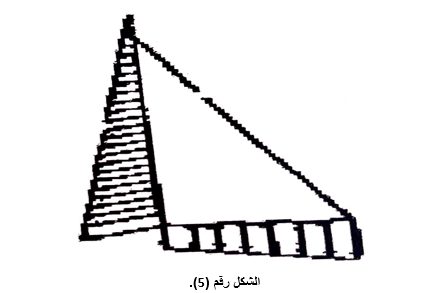
تستخدم العوامل K الموضحة فب الشكل رقم (5) من أجل حساب عزوم الانعطاف M= K.q².a².

يتم تصميم بلاطة القدم كبلاطة ظفرية موثوقة إلى الجزع كما هو الحال في الجدران الاستنادية الظفرية.

أما الدعامات فمن الممكن أن تصمم على أنها ظفر موشوري الشكل موثوق إلى القاعدة ومعرض إلى ردود فعل أفقية من بلاطة الجزع وردود فعل شاقولية من بلاطة الشكل رقم (5).

أو تصمم الدعامة كجزء متكامل مع بلاطة الجزع وتدرس عندئذ على أنها جائز بمقطع T مضغوط الأجنحة يوضح الشكل رقم (6) ترتيبات التسليح وبعض التفاصيل الإنشائية للجدران الاستنادية المدعمة.&

​