& من الحالات التي نصادفها لدى دراسة أساسات مرنة غير محددة الطول ما يلي:
- حالة تأثير حمولة خارجية مركزة ووحيدة على أساس جائزي غير محدد الطول له صلادة ثابتة يستند على تربة عامل صلابتها غير متغير.
ليكن لدينا الأساس الجائزي المستمر فيه مبدأ الجملة الإحداثية يقع عند مركز تأثير الحمولة الشاقولية كما موضح بالشكل رقم (1).
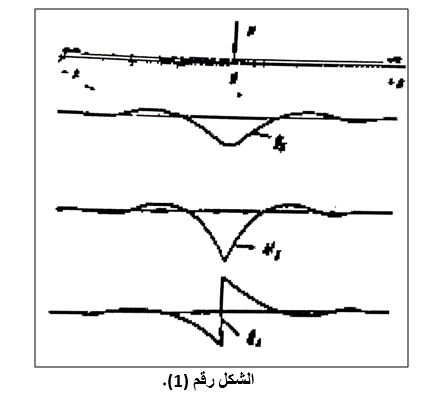
تكون المعادلة التفاضلية لانحناء الأساس من الشكل:

حيث: y1,y2,y3,y4 تسمى توابع كريلوف لهم القيم التالية:
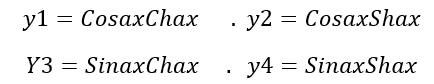
بالدراسة نعتمد الحل العام المحدد بالمعادلة الأخيرة.
لتحديد الثوابت الأربعة فإنه يجب تطبيق أربعة شروط طرفية:
الشرط الأول: عند مسافة كبيرة (غير محددة) من موقع تأثير الحمولة فإنه يقترب تشوه الأساس من الصفر بالتعويض بقيمة * في الحل العام فإننا نحصل على تناقض لأن قيمة ![]() ستبلغ قيمة غير محددة لا تساوي مطلقا الصفر فلذلك حتى يتحقق ذلك يجب أن يكون : C1= C2= 0 وبالتالي معادلة تشوه الأساس تصبح:
ستبلغ قيمة غير محددة لا تساوي مطلقا الصفر فلذلك حتى يتحقق ذلك يجب أن يكون : C1= C2= 0 وبالتالي معادلة تشوه الأساس تصبح:

فباشتقاق معادلة تشوه الأساس ثلاث مرات والتعويض نجد:









