المميزات العامة للجمل المقررة ستاتيكيا وغير المقررة
تكون الجملة مقررة ستاتيكيا إذا كانت معادلات التوازن كافية لتعيين ردود الأفعال في مساند هذه الجمل ، وكافية لتعيين القوى الداخلية في عناصرها ويعتمد في حل هذه المسائل معادلات التوازن الثلاثة التالية :
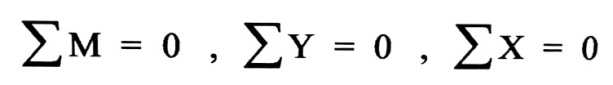
وتتصف الجمل المقررة ستاتيكيا بالصفات العامة التالية :
- ردود الفعل في مساند هذه الجمل لا تتوقف على صلابة عناصرها أو اختلاف هذه الصلابة .
- تغير درجة حرارة بعض عناصر هذه الجمل أو الجملة بأكملها لا يؤدي إلى ظهور إجهادات جديدة .
- هبوط المساند لا يولد في عناصر هذه الجمل أية قوى داخلية .
- عدم الدقة في صنع عناصر الجملة لا يولد في هذه العناصر إجهادات ابتدائية .
والشكل رقم (1) يبين مثالين لهذه الجمل .
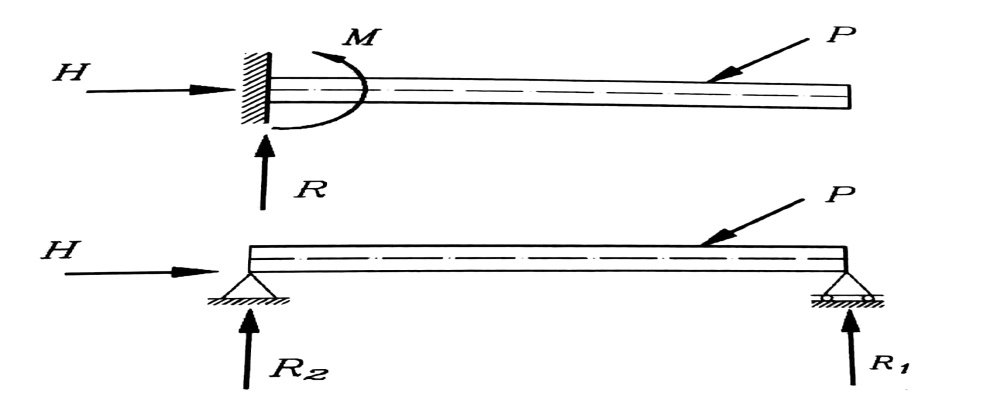
الشكل رقم (1)
المميزات العامة للجمل غير المقررة ستاتيكيا :
يطلق اسم الجمل غير المقررة ستاتيكيا على الجمل التي لا تكفي معادلات التوازن لتعيين ردود الأفعال في مساندها وبالتالي لتعيين الإجهادات فيها ، وفي مثل هذه الجمل لا بد من معادلات إضافية غير معادلات التوازن ونحصل على هذه المعادلات من شروط تشوه الجملة المدروسة .
وتتصف هذه الجمل بصفات عامة هي :
- إن الحالة الإجهادية في عناصر الجملة غير المقررة ستاتيكيا تتوقف على نسب مقاطع هذه العناصر بعضها إلى بعض ، فالمقطع الأكبر يأخذ القسم الأكبر من الحمولة ، والمقطع الأصغر يأخذ الجزء الأصغر منها .
- إن تغير حرارة العنصر بعد تنفيذه في الوقت الذي تبقى فيه حرارة المساند ثابتة يولد إجهادات في العنصر .
- إن هبوط أحد المساند يولد إجهادات إضافية في المنشأ .
- إن عدم الدقة في تصنيع أحد عناصر المنشأ يولد إجهادات ابتدائية في هذا المنشأ .
وتدرس الجمل غير المقررة ستاتيكيا في حالة الشد والضغط ، كما ندرس تأثير الحرارة وعدم الدقة في صنع العناصر على الجمل غير المقررة ستاتيكيا .
مثال :
ليكن لدينا عنصر أفقي مطلق الصلابة ومعلق بواسطة ثلاثة قضبان . تؤثر على العنصر الأفقي قوة عمودية على محوره ومطبقة في منتصفه مقدارها P ، كما هو موضح في الشكل رقم (2) .
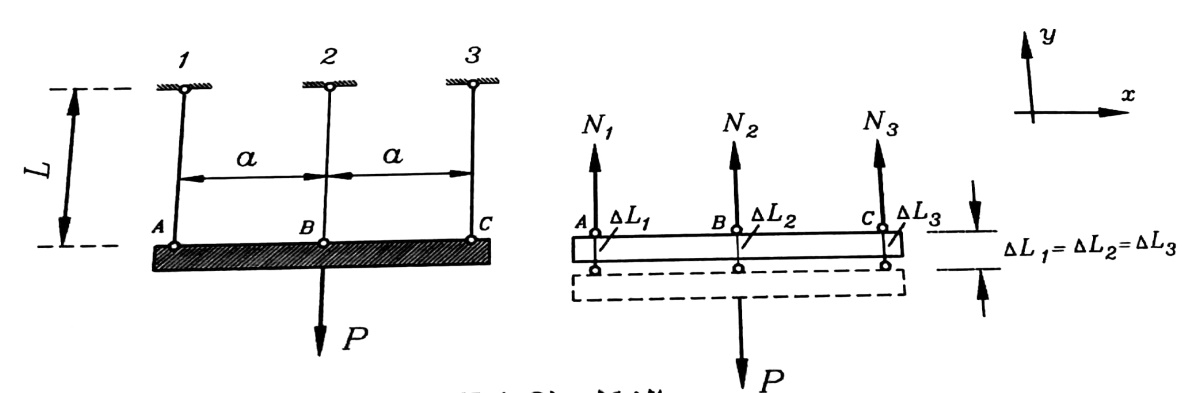
الشكل رقم (2)
بفرض أن هذه القضبان منفذة من مادة واحدة ولها معامل مرونة ثابت E ومساحة كل منها تساوي A ويبعد القضيب الاوسط مسافة a عن القضيبين الطرفيين ، والمطلوب تحديد القوى الداخلية في القضبان الثلاثة من جراء تأثير القوى الخارجية P .
نلاحظ أن الجملة غير مقررة ستاتيكيا من الدرجة الأولى (مرة واحدة فقط) وذلك لوجود ثلاث قوى داخلية غير معلومة في العناصر الثلاثة وفق طريقة القطع . بينما في الجملة المستوية لحالة القوى المتوازنة لدينا معادلتان للتوازن :
الأولى : هي مجموع مساقط جميع القوى على المحور oyلجميع القوى المؤثرة على القسم المقطوع يجب أن يساوي الصفر .
الثانية: المجموع الجبري لعزوم هذه القوى حول أية نقطة يجب أن يساوي الصفر .
وأما معادلة التوازن الثالثة فتؤول إلى الصفر . ومن هاتين المعادلتين لا يمكن تحديد ثلاث قوى مجهولة .









