حساب الجوائز غير المقررة استاتيكيا من الدرجة الأولى
إن حساب هذه الجوائز يتطلب تشكيل معادلة تشوه إضافية واحدة ، وطريقة الحساب مبينة في الأمثلة التالية :
مثال (1) :
إن أحد أشكال الجملة الرئيسية للجائز المبين بالشكل رقم (1-a) موضح في الشكل رقم (1-b) حيث تم الاستعاضة عن الوثاقة بمسند مفصلي ثابت وعزم انعطاف مجهول ma .
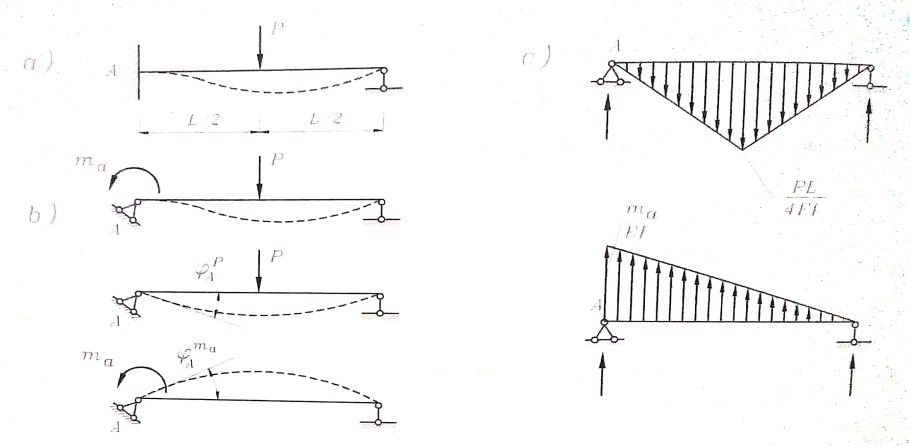
الشكل رقم (1)
إن معادلة التشوه في هذه الحالة : ϕa = 0 ، أي :
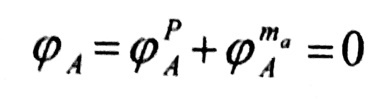 (1)
(1)
حيث :
ϕAP : زاوية دوران المقطع A في الجملة الرئيسية من تأثير القوة P .
ϕAma : زاوية دوران المقطع A في الجملة الرئيسية من تأثير العزم المجهول ma .
وتعبر المعادلة رقم (1) عن أن زاوية دوران مقطع الجائز عند المسند A ، من تأثير القوة P والعزم المجهول ma ، تساوي الصفر ، وهذا مطابق لحالة الجائز الأصلي حيث A وثاقة .
إن تشوه الجائز تحت تأثير كل من القوة P والعزم ma على حدة يظهر في الشكل رقم (1-b) ، ولتحديد زاويتي دوران المقطع ϕAP ، ϕAma يفضل استعمال طريقة الجائز المرافق . والجائزان المرافقان والمحملان بالحمولتين المرنتين التخيليتين موضحان في الشكل رقم (1-c) والمعادلتين :
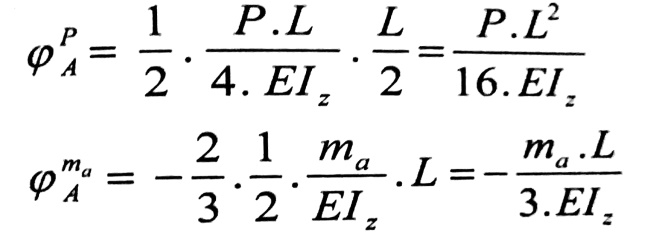
نلاحظ أن ϕAma < 0 وذلك لأن المقطع يدور عكس عقارب الساعة ، بتعويض قيمتي ϕAP و ϕAma بالمعادلة رقم (1) ، نجد :
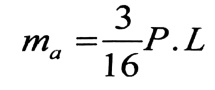
وبهذا أصبح بالإمكان رسم مخطط MZ و Qy بالطرق المعروفة بالجوائز المقررة استاتيكيا ، ويبين الشكل رقم (2) مخططي MZ و Qy .
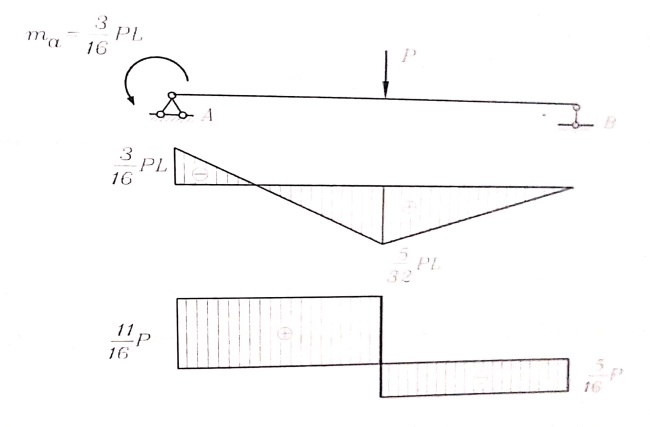
الشكل رقم (2)
مثال (2) :
يبين الشكل رقم (3-a) جائزا محملا بحمولة موزعة بانتظام q . عند اختيار الجملة الرئيسية من الأفضل حذف المسند B والاستعاضة عنه برد الفعل المجهول Rb ، الشكل رقم (3-b) .









