قاعدة تشبيشف

تهدف هذه الطريقة إلى إيجاد علاقة أو معادلة بسيطة تسمح بأجراء التكامل الرقمي التقريبي بأعلى دقة ممكنة.

لتحقيق الشرط الأول ينبغي ألا تحتوي العلاقة على معاملات تكامل التي تضرب بها الإحداثيات الرأسية، لتحقيق الشرط الثاني ينبغي استبدال المنحني المحيط بالسطح المدروس بتابع من الدرجات العليا.

تعتمد فكرة هذه الطريقة على اختيار عدد محدد من الإحداثيات الرأسية للمنحني المحيط بالشكل المدروس بحيث إن جداء القيمة الوسطية لهذه الإحداثيات الرأسية للمنحني المحيط بالشكل المدروس بحيث أن جداء القيمة الوسطية لهذه الإحداثيات بطول الشكل المدروس يساوي لمساحة هذا الشكل.

يتم اختيار المحور oy وفقا لهذه الطريقة في منتصف طول الشكل المعطى، أي أن الاحداثيات الافقية x₁  ٍستأخذ قيماً سالبة وموجبة كما في الشكل التالي:

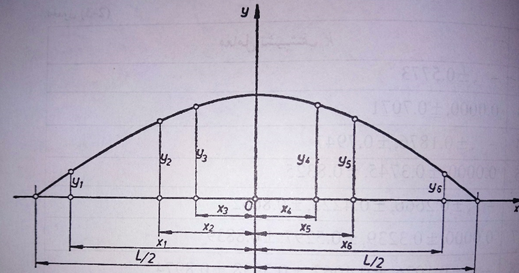
ومنه:

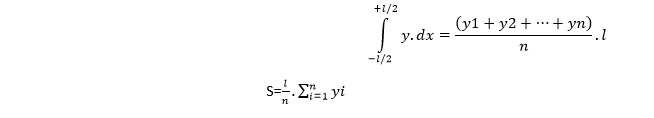
حيث أن:

L: يمثل طول الشكل المدروس أو مجال التكامل

n: عدد الإحداثيات الرأسية المستخدمة في الحساب.

إن حل هذه المسألة (بدون التطرق إلى التفاصيل الرياضية المعتبرة) قاد إلى توزيع الإحداثيات الرأسية المستخدمة بالنسبة لمنتصف طول الشكل المعطى وفق العلاقة:

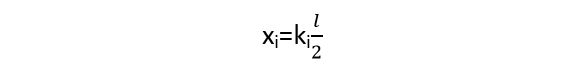
حيث إن:

K_i: معامل تشيبشف ويتعلق بعدد الإحداثيات الرأسية المختارة.

يتطلب استخدام هذه الطريقة أعمالاً إضافية خاصة بتحديد الاحداثيات الرأسية من رسمة الخطوط النظرية نظراً لكون الإحداثيات الرأسية (اعتباراً من 5 فما فوق) وبما أن الحسابات الجارية غير معقدة، فإنه يرغب باستخدامها خصوصاً عند حساب مساحات سطح الطفو فعند اختيار 8 إحداثيات رأسية ستتطابق تقريباً الإحداثيات الأفقية المحددة بهذه الطريقة مع الإحداثيات الأفقية المقابلة لحالة التقسيم العشري المستخدم عادة للخطوط النظرية (أي تقسيم طول السفينة الى 10 أجزاء فإن أرقام الإحداثيات الأفقية المعينة هي: 2/1 ,2 ,3 , 2/1 4 ,2/1 5 , 7 , 8 , 2/1 9 ) لهذا السبب يمكن استخدام طريقة تشيبشف بدقة كافية عندما