نمذجة الأنظمة متعددة المعالجات - الجزء الأول 

 **نمذجة الأنظمة متعددة المعالجات**

&  تعتبر  نمذجة الأنظمة ذات دور هام في تحديد فعالية الأنظمة و تعقيدها ,وتعطي رؤية معمقة عن سلوكية الأنظمة. و يمكن أن تعتمد أسلوباً لفهم مشكلات التزامن والتوازي ,وهو المحاكاة التي تعتبر طريقة عامة تقريباً على كل الأنظمة.

إذ أن معظم سلوكيات الأنظمة تتشابه فيما بينها ,و بالرغم من أن المحاكاة اقتصادية أكثر من إنشاء الأنظمة مباشرةً, إلا أن هذا الأسلوب يعتبر بطيئاً و ذو كلفة مرتفعة نسبياً إضافةً لذلك فهي تعطي معلومات محدودة عن العلاقة المنطقية بين سلوكية النظام المحاكي و صفات النظام الحقيقي.   &

**نماذج الحساب المتوازي**

& يمكن أن نوضح مفهوم الحساب المتوازي بتعريف بعض النماذج , التي نقوم باستعمالها لتقديم أفكار ونتائج تشكل أساسات نظرية الحساب المتوازي.     &

**نظريات الحساب المتوازي**

&     وهي تعرف أن المكان والزمان هما المصدران الأساسيان الأكثر أهمية المعرفان لتعقيد الحساب التسلسلي، وفي الحساب المتوازي تبقى أهمية الزمن نفسها:

حيث أن السبب الرئيسي لدراسة الحساب المتوازي هو للحصول على زيادة سرعة حل المسائل الحسابية up  speed ، و بشكل بديهي يمكننا أن ندرك ببساطة أنه إذا توفر لدينا وحدات معالجة أكثر فإن الزمن المطلوب لحل مسألة معطاة ينخفض، و هذه الحقيقة تجعل وحدات المعالجة هي المتطلب الرئيسـي الحالي في الحساب المتوازي.

بالإشارة إلى النموذج الذي نعالجه فإن هناك العديد من مجموعات وحدات المعالجة لكمية متوفرة من المكونات الصلبة. وهذه المكونات الصلبة للحاسوب هي الوحدة الأكثر عمومية في القياس ,و التي يمكن في بعض الحالات أن تتطابق مع عدد وحدات المعالجة.

الفكرة القائلة أن الزمن والمكونات الصلبة هما القياسان الرئيسيان للحساب المتوازي , مستندة على عدة نتائج مرتبطة بمصادر تسلسلية للمكان و الزمان على التوالي مع الزمن و المكونات الصلبة في الحالة المتوازية.  

التطابق الذي تحدثنا عنه سابقاً, و الموجود بين المكان والزمان في أي نموذج اعتيادي للحساب المتوازي , يعطي نظرية الحساب المتوازي، و بالأخذ بعين الاعتبار أن جميع نماذج الحساب التسلسلي تتصل ببعضها بشكل متعدي , يمكننا عندئذ أن نعبر عن فرضية الحساب المتوازي كما يلي:

إن  أي آلة حساب تورنك مع كلفة مكانS(N)  يمكن أن تحاكى على نموذج عادي للحساب المتوازي بكلفة زمنية:

 T(N) =O(S(N)^c)

وبالعكس فإن أي حساب على نموذج عادي للحساب المتوازي مع كلفة زمنية (T)n يمكن أن يحاكى بواسطة آلة حساب تورنك بكلفة مكانية S(N) =O(T(N)^d) حيث  d,c  هي ثوابت تابعة للنموذج.   &

**الحسابات المتوازية و النماذج اللوغاريتمية**

&  تعتمد معظم لغات البرمجة عالية المستوى على آلة خاصة صممت في بنية الحاسب المعتاد. تدعى هذه اللغات قاعدية imperative ، و يعرف البرنامج على أنه أوامر تسلسلية أساسية للمعالج، كما أن بنية الحاسب المعتاد نفسها تعتمد على النظرة التسلسلية للحسابات.

ومن وجهة منطقية يمكن أن نعتبر بعض خطوط البرنامج مستقلة حتى إذا كانت تسلسلية فيزيائياً.

لنأخذ برنامج ضرب مصفوفتين من الحجم n  و هو برنامج خطي مستقيم يعبر عن الحالة n=2  و هو كالتالي :

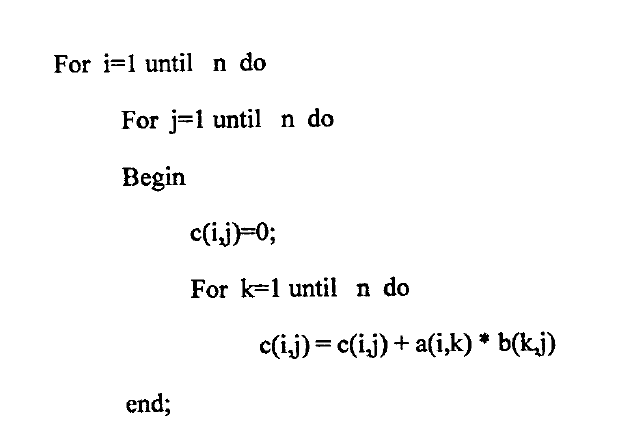
    سنبين الآن خطوات التي يتم فيها تنفيذ البرنامج و كيف تأخذ عناصر المصفوفة الناتجة قيمها و ذلك كالآتي :