كفاءة الخوارزمية
إن التعريف الأكثر انتشاراً و رواجاً لمفهوم كلفة الخوارزمية ,هو أنها حاصل جداء عدد المعالجات المستعملة لإنجاز العملية و بين زمن تنفيذها , إن حل الجمل الكبيرة من المعادلات الخطية يمكن أن يكلف كثيراً على الحاسب.
وحتى نعرف لماذا , سننجز عملية عد لخوارزمية لها كود معطى. سنعد فقط عمليات الضرب والقسمة (العمليات الطويلة) لأن لها أكبر زمن مستهلك، بعد ذلك نجمع عمليات الضرب والقسمة معاً حتى ولو كانت عمليات القسمة أبطاً من عمليات الضرب.
مثال : لنأخذ خوارزمية Gauss الذي نقوم فيه بحل جملة معادلات خطية ومن ثم نقوم بحساب الكلفة وذلك بعد العمليات الطويلة فيه، و فيه مصفوفة الأمثال .. (aij)nnو مصفوفة الثوابت (ij)nوهناك مصفوفة مساعدة لتحديد مواقع العناصر هي (si ) n.


حساب كلفة الخوارزمية السابقة
وفيما يلي نحسب كلفة تنفيذ الخوارزمية السابقة :
في الخطوة 1: يتطلب اختيار العنصر المحوري حساب n نسبة وهذا يعني: n مقسوم و من ثم من أجل الأسطر I1,I2,…….In نبدأ أولاً بحساب الضرب و من ثم نطرح من السطر 1i مرات الضرب و هي السطر 11
أما الصفر الذي ينشأ من هذه العملية فلا يحسب , و منه يتطلب الحذف n-l مضروب في كل سطر إذا ضمنا حساب المضاريب فإننا نجد 1-n عملية طويلة (مقاسيم و مضاريب) في كل سطر و نجد أن هناك 1-n سطر يجب معالجتها لنحصل بالنتيجة على n(n-1) عملية.
إذا أضفنا كلفة حساب النسب فإن النتيجة هي n2 عملية مطلوبة من أجل الخطوة 1 .
الخطوة التالية مثل الخطوة l ما عدا أن السطر i1 لا يؤثر بل على العكس فإن عمود المضاريب قد نشأ وخزن في الخطوة1 , لذلك فإن الخطوة 2 ستتطلب2 (1-n) مضروب و مقسوم تتم معالجتها على الجملة مع السطر i1 بدون العمود1 , باستمرار هذه المعالجة نحصل على أن نتيجة عدد العمليات الطويلة للإجراء Gauss هي:
N2+(n-1)2+(n-2)2+……..+42+32+22=n/6(n+1)(2n+1)-1=n3/3
لاحظ أن عدد العمليات الطويلة في هذا الإجراء ينمو إلى n3/3 .
نظرية: إن الحذف المتقدم المتجانس لخوارزمية حذف غاوس مع تخفيض المحاور الجزئية إذا طبقت فقط على مصفوفة معاملات nn تقريباً ب n3/3 عملية طويلة (ضرب و قسمة). و الحل من أجل x يحتاج n2 عملية إضافية طويلة.
لنقوم الآن بإيجاد خوارزمية متوازية لمسألة حل جملة معادلات خطية ,و سنستخدم طريقة غاوس جوردان حيث أنها الطريقة التسلسلية الأكثر شيوعاً لحل هذه المسألة، و هي تتألف من حذف المجاهيل x ما عدا xi من المعادلة i و بذلك نحصل على الحل مباشرة.
الخوارزمية المتوازية لطريقة غاوس جوردان مصممة لتنفذ على حاسب CREW SIMD SM ب n+n2 معالج يفترض بأنها مرتبة في مصفوفة n(n+1) تعطى الخوارزمية كإجراء JORDAN SIWIDGAUSS. ونرمز فيها لـ bi بـ ai,n+1
الإجراء SIMD GAUSS JORDAN (A,b,x)
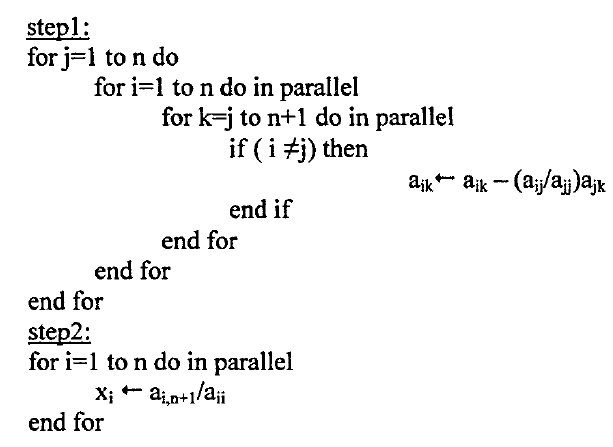
نلاحظ أن الإجراء يسمح بعمليات القراءة المتعددة لأكثر من معالج واحد وذلك عندما يحتاج لقراءة aij و ajj و ajk بآن واحد.









