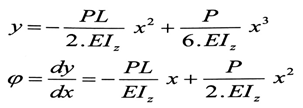أمثلة تطبيقية حول المعادلة التفاضلية لمحور الجائز المنحني (الخط المرن)
مثال 1 :
اكتب علاقة السهم و زاوية الدوران في مقطع اختياري يبعد بمقدار x عن مبدأ الإحداثيات للجائز الظفري المحمل بقوة مركزة P تؤثر على طرفه ، الشكل رقم (1) .
ملاحظة : اصطلاح إشارة السهم وزاوية الدوران :
يكون السهم موجبا إذا كان باتجاه المحور y ، وتكون زاوية الدوران موجبة إذا كان ميل المماس للخط المرن يقع بالربع الموجب (الأول والثالث) للجملة الإحداثية المفروضة .
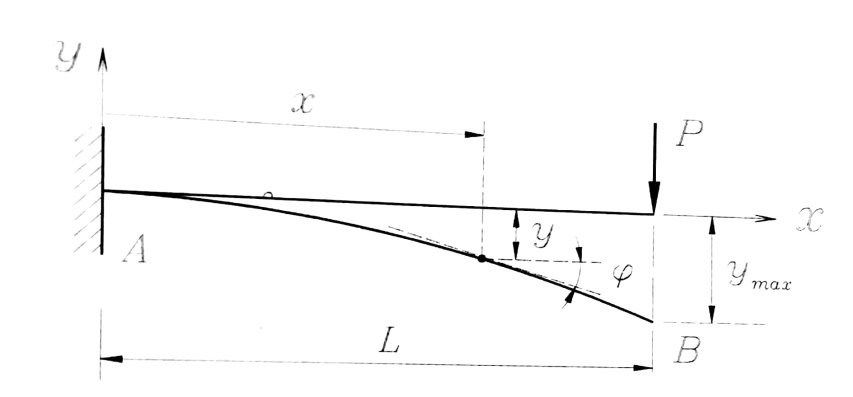
الشكل رقم (1)
الحل :
إن قيمة عزم الانعطاف في هذا المقطع :
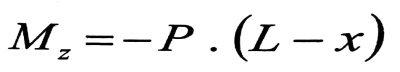
الإشارة السالبة أخذت لأن الألياف السفلية مضغوطة ، وبما أن المحور y يتجه إلى الأعلى فإن الحد الأيمن من المعادلة التفاضلية رقم (5) من مقال( تعيين الإزاحات في الجوائز المعرضة للانعطاف) يجب أخذه بالإشارة الموجبة .
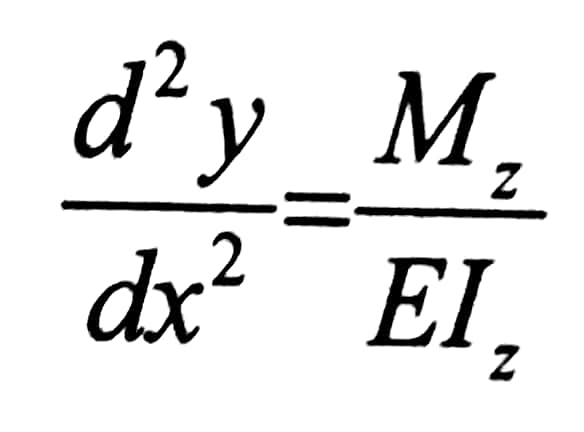
بتعويض قيمة Mz ، نجد :
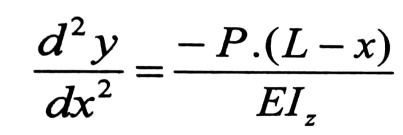
بفرض أن صلابة الجائز ثابتة ، بالمكاملة لمرة واحدة ، نجد:
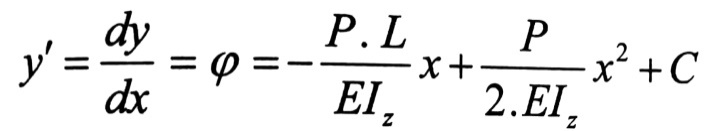(1)
بالمكاملة لمرة ثانية ، نجد :
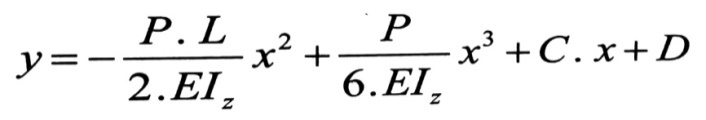(2)
بما أن السهم وزاوية الدوران عند الوثاقة يساويان الصفر ، فلتحديد ثوابت التكامل يكون لدينا الشروط الطرفية التالية :
من العلاقة رقم (1) نلاحظ أن الثابت C هو عبارة عن قيمة زاوية الدوران في مبدأ الإحداثيات ، بالتعويض بقيمة X= 0 ، نجد : C= 0 .
وبالمثل في المعادلة رقم (2) نجد أن الثابت D هو عبارة عن قيمة السهم في مبدأ الإحداثيات ، بتعويض X=0 نجد : D=0 ، وبهذا تصبح المعادلات بالشكل :
قم بتنزيل تطبيق eMufeed Android الآن
