الحالة الإجهادية المحورية
لتقدير متانة المادة ومعرفة شكل انهيارها نحتاج لتحديد قيمة الإجهادات التي تؤثر في أي مقطع مائل من القضيب المشدود أو المضغوط .
ومن أجل ذلك نقطع القضيب بمستو يميل على المقطع العرضي بزاوية α ، الشكل رقم (1) .
ملاحظة : الزاوية α يمكن اعتبارها ، أيضا ، بين محور القضيب والناظم على المستوي .
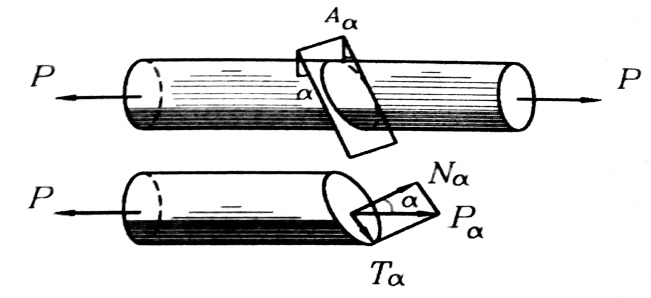
الشكل رقم (1)
يمكن التعبير عن مساحة المقطع المائل Aa من خلال مساحة المقطع العرضي A ، بالعلاقة :
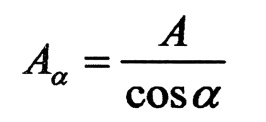
ومن شرط توازن القسم الأيسر للمقطع المدروس ، الشكل رقم (1) ، نجد أن محصلة القوى الداخلية في المقطع المائل Pa تساوي القوة الخارجية P ، أي : Pa = P
ونحلل القوة Pa إلى مركبتين :
- المركبة الأولى ناظمية Na وهي تشكل الإجهادات الناظمية في المستوي المائل .
- المركبة الثانية مماسية Ta وهي تشكل الإجهادات المماسية في المستوي المائل .
إن التوزع المنتظم لهاتين المركبتين على المساحة Aa للمقطع المائل يؤديان إلى نشوء إجهادات ناظمية ومماسية في كل نقطة من نقاط هذا المقطع وقيمة هذه الإجهادات :
مع الأخذ بعين الاعتبار أن :
وبالتعويض في علاقتي الإجهادات ασ و αꚌ السابقة بعد الأخذ بعين الاعتبار أن :
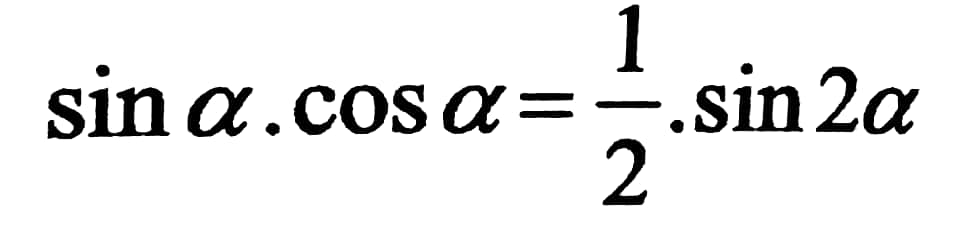
نحصل على :
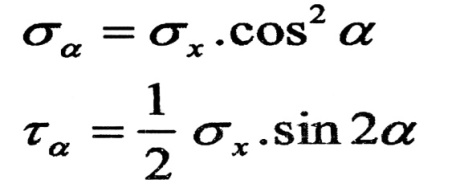
أي أن الإجهادات على مستو مائل على محور قضيب معرض لشد محوري ، تتعين بالعلاقتين :
قم بتنزيل تطبيق eMufeed Android الآن
