إن المعادلة ثنائية الحد أدق من معادلة "رولينس و شیلهارت" الأسية وتتعلق دقة هذه المعادلة بمجالات الضغوط والحرارة .
• معادلة (a) بالوحدات المترية هي :
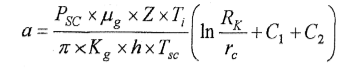
معادلة (a) بالوحدات الحقلية (الإنكليزية):
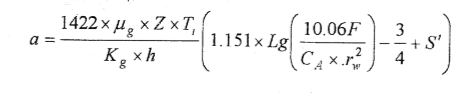
حيث إن :
ß: عامل الاضطراب و يحسب من علاقة شیرکوفسكي :
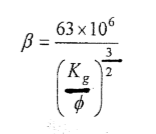
و معادلة (b) بالوحدات الحقلية :
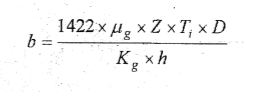
حيث أن :
Psc : الضغط القياسي بالباسكال .
gɥ : لزوجة الغاز ، تقاس بالوحدات المترية بالباسكال ثانية.
Ti : درجة الحرارة الأولية ، تقاس بالوحدات المترية بالكلفن (K) .
Kg : نفوذية التشكيلة تقاس بالوحدات المترية ب (m²) أو (Darcy1012 ) .
ϴ : المسامية كجزء من الواحد .
h : السماكة الفعالة للتشكيلة تقاس بالوحدات المترية بالمتر .
Tsc : درجة الحرارة القياسية بالكلفن .
Rk : نصف قطر منطقة السحب بالمتر .
rc : نصف قطر البئر بالمتر .
C1 : عامل يأخذ بعين الاعتبار عدم تمامية البئر من حيث درجة فتحها ، ويمكن الحصول عليه من جداول ومنحنيات خاصة أو من العلاقة الآتية :
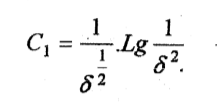
ϭ: نسبة اختراق الطبقة وتحسب من العلاقة: ϭ = B / h
B : السماكة المخترقة .
C2: عامل يأخذ بعين الاعتبار عدم تمامية البئر من حيث طبيعة فتح الطبقة . ويحسب بالصيغة التقريبية للباحث "مينسك .ي.م" :
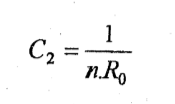
n : عدد الثقوب لكل متر واحد من سماكة الطبقة .









