قانون هوك المعمم 

  قانون هوك المعمم

حتى الآن تم دراسة الحالتين الإجهادية (σ_x , σ_y , σ_z , Ꚍ_xy , Ꚍ_xz , Ꚍ_yz) و التشوهية (Ꜫ_x , Ꜫ_y , Ꜫ_z , Y_xy , Y_xz , Y_yz) الحجمية ، كلا على حدة ، ولم نربطهما بصفات المادة . إلا أنه بين مركبات الحالة الإجهادية ومركبات الحالة التشوهية توجد علاقة معينة .

هذه العلاقة تكون خطية في حدود التشوهات الصغيرة وتدعى هذه العلاقة بقانون هوك المعمم .

ولاستخراج العلاقة التحليلية لقانون هوك المعمم (يقصد بقانون هوك المعمم العلاقة بين التشوهات والإجهادات في الحالة الإجهادية المستوية والحجمية) سنعتمد على مبدأ استقلال تأثير القوى وسندرس القوى المؤثرة على جوانب عنصر مكعب كلا على حدة ، الشكل رقم (1) .

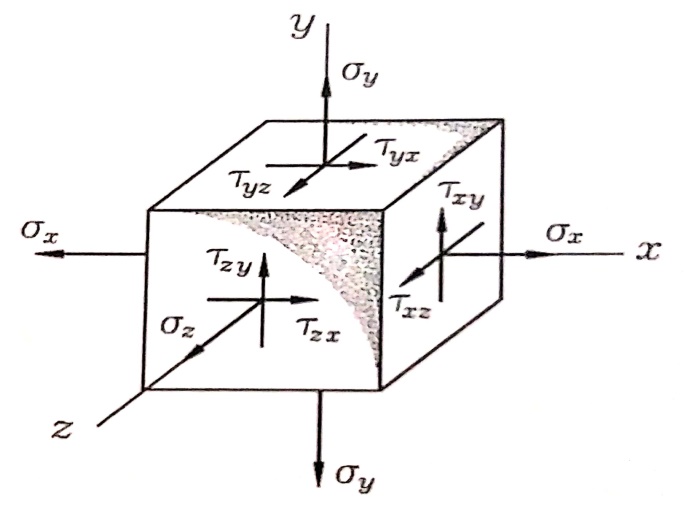
الشكل رقم (1)

وبدون برهان سنذكر بعض النتائج الأساسية والتي تصح فقط للجسم الإيزوتروبي :

- إن التشوهات الزاوية (, Y_xy , Y_xz , Y_yz) تتعلق فقط بالإجهادات المماسية (Ꚍ_xy , Ꚍ_xz , Ꚍ_yz) الواقعة في مستوي كل منهما على التوالي فقط .

- إن التشوهات الزاوية (, Y_xy , Y_xz , Y_yz) لا تتعلق بالإجهادات الناظمية (σ_x , σ_y , σ_z) .

- إن التشوهات الخطية (Ꜫ_x , Ꜫ_y , Ꜫ_z) لا تتعلق بالإجهادات المماسية (Ꚍ_xy , Ꚍ_xz , Ꚍ_yz) .

- إن التشوهات الخطية (Ꜫ_x , Ꜫ_y , Ꜫ_z) تتعلق فقط بالإجهادات الناظمية (σ_x , σ_y , σ_z) .

فمثلا في المستوي الإحداثي xoy ، يتعين التشوه الزاوي  Y_xyبدلالة الإجهادات المماسية Ꚍ_xy الموافقة لها ، أما بقية الإجهادات المماسية وكذلك الناظمية فإنها لا تؤثر على قيمة Y_xy وذلك بسبب صفات الجسم المتماثل (الجسم الإيزوتروبي) .

- من تلك النتائج نستطيع أن نكتب العلاقة بين التشوهات الزاوية والإجهادات المماسية في الحالتين المستوية والحجمية :

أولا: في الحالة الإجهدية :

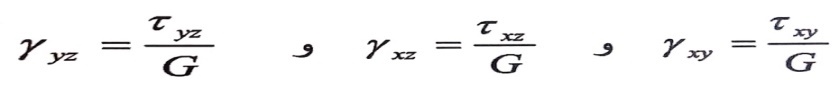
ثانيا: في الحالة الإجهادية المستوية :

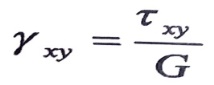
أما الدراسة العلاقة بين الإجهادات الناظمية والتشوهات الخطية ، وللسهولة ، سنستخرج تلك العلاقة اعتمادا على حالة إجهادية رئيسية مستوية ثم نعممها على الحالة الإجهادية الحجمية .

نحدد التشوهات النسبية Ꜫ₂ , Ꜫ₁ في اتجاهات الرئيسية في الحالة الإجهادية المستوية (ثنائية المحور) ، الشكل رقم (2) . ولأجل هذا نستعمل قانون هوك لحالة الإجهاد الوحيد امحور ، وبالتالي العلاقة التي تربط بين التشوهات الطولية والعرضية وكذلك مبدأ تراكب القوى (مبدأ جمع التشوهات ) .

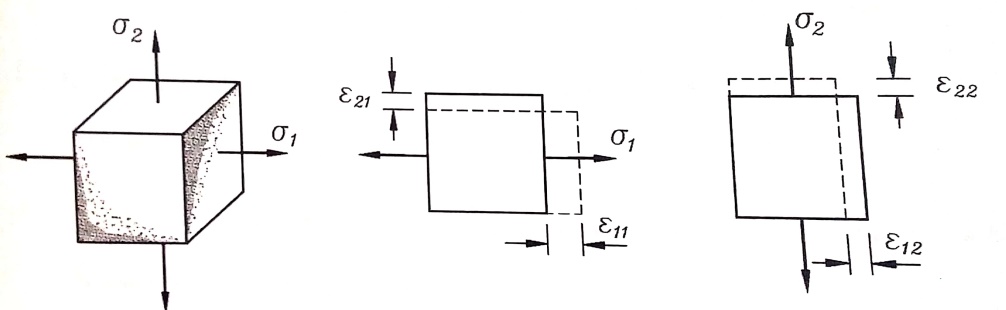
الشكل رقم (2)

بتأثير الإجهاد ₁σ وحده فقط ، فإن الاستطالة النسبية باتجاهه تساوي :

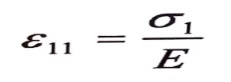
بنفس الوقت ، فإن التقلص النسبي في الاتجاه العمودي عليه يساوي :