نمذجة الأنظمة متعددة المعالجات - الجزء الثاني

**تعريف النموذج اللوغاريتمي**

&   يبدأ هذا النموذج من شروط برنشتاين لاحتمال توازي الخوارزميات ( ولا يهتم بالتفاصيل) ويمكن وصفه بالحقائق التالية:

1- يمكن أن يستعمل أي عدد من المعالجات في أي لحظة.

2- يمكن أن ينفذ كل معالج أي تعليمة (رياضية أو منطقية) في وحدة زمن.

3- لا يوجد كلفة من أجل الوصول البيانات.

4- لا يوجد كلفة للاتصال بين المعالجات.

أما المصادر الأساسية المطلوبة من النموذج فهي عدد الخطوات المتوازية (عدد وحدات الزمن) وعدد المعالجات المستعملة كدالة في حجم المسألة.    

مثال : يمكن أن نتحقق من قواعد تعريف النموذج اللوغاريتمي ونطبقها على خوارزمية حساب ناتج جداء  مصفوفتين و تحليل الكلفة الناتجة :

الدخل : مصفوفتين   A=(aij) و  B=(bij ) من الحجم n  .

الخرج : مصفوفة C=(cij )  من الحجم n حيث C=AB

الخطوات:

1. حساب ال n3 ناتج على التوازي حيث : t_aj = a_ik * b_kj
2. حساب الn2  مجموع على التوازي حيث : Ij=1…..n , c_ji=t_i1j+ t_i2j+……+t_inj

 المخطط التالي للتوضيح و نرمز فيه ب tk بدلاً من tikj  و فيه n=8 و هو في الشكل التالي :

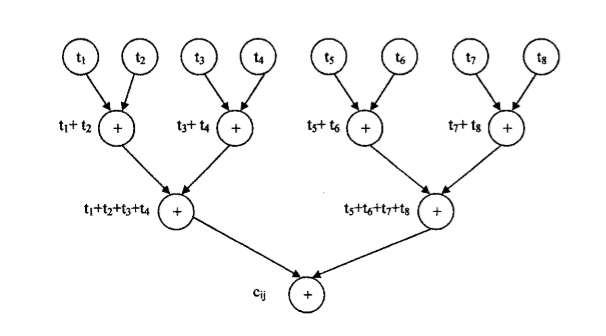
• الكلفة:

الخطوة 1 تتطلب وحدة زمن واحدة و n3 معالج.

الخطوة 2 تطلب [log n] + 1 خطوة و n3 معالج مطلوب.

عندما يكون العدد p من المعالجات ثابتاً يكون التوازي منتهياَ.

يمكن تحليل انجاز الخوارزمية عن طريق مقياسين آخرين وهما: زيادة السرعة و الفعالية.

زيادة السرعة up  speed ونرمز لها Sp(n) تعرف بأنها النسبة بين كلفة الزمن لأفضل خوارزمية تسلسلية متوفرة, وكلفة الزمن لخوارزمية التوازي التي نحللها.

 عندما تكون خوارزمية التوازي تملك على الأغلب p  معالج متوفر فإن: Sp(n)=T1(n)/Tp(n)  حيث n هو حجم المسألة.

 مما سبق نلاحظ أن أفضل حالة لهذا الشرط هو عندما يكون p Sp(n) = وذلك من الصعب الوصول إليه عملياً. و المطلوب هو الحصول على مسألة تحل بزمن تسلسلي T(n) أن تحل بزمن متوازي T(n)\pحيث p هو عدد المعالجات المتوفرة.

إضافةً إلى أنه يوجد زمن ما لا محالة في الحساب المتوازي , يستعمل لتنسيق فعالية المعالج. ويتحدد التوازي تبعاً لطبيعة المسألة نفسها.

الفعالية (efficiency) و نرمز لها (E)n و هي النسبة بين زيادة السرعة وعدد المعالجات , Ep(n)=Sp(n)\p من الواضح أن Ep(n)<=1  وتتحقق أفضل فعالية عندما تطبق شارة التساوي.

يطبق مفهوم زيادة السرعة و الفعالية عند دراسة التوازي ,و في تحليل الخوارزميات عندما يزداد عدد المعالجات مع حجم  المسألة، في هذه الحالة نجعل p=p(n) وتحسب زيادة السرعة والفعالية كما لو أن p    ثابت.

   في هذا النموذج نحاول الحصول على المعلومات التالية:

1- القيم من الحجم n التي من أجلها يكون إنجاز الخوارزمية أفضل.

2- السلوك المقارب لزيادة السرعة والفعالية.

في المثال السابق تعطى زيادة السرعة والفعالية كما يلي:

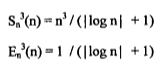
 نلاحظ أن الفعالية تتلاشى عند اللانهاية   ∞هذا يعني أن n هي الأعظمية الزمن الأطول ,الذي تكون خلاله معظم المعالجات غير فعالة.

وهكذا نجد أن الاقتراحات السابقة هي احتمالات لدراسة الخوارزميات المتوازية. أحدها للتفكير في العدد  p   لوحدات المعالجة المتوفرة كثابت ,ولمحاولة تأليف خوارزميات متوازية مع زمن تنفيذ Tp(n)     يرفع زيادة السرعة إلى الحد الأعلى. من جهة أخرى  يمكن أن يكون كدالة في حجم الإدخال أي أن p=p(n)  ,و يمكن تجريب خوارزميات تحتاج أقل احتمال لزمن متوازٍ.&

**الدارات المنطقية**

&  قبل أن تبدأ الدراسات حول التوازي ,كانت تستعمل الدارات المنطقية بشكل كبير عندما ندرس تعقيد الحسابات ونستعمل طول الدالات المنطقية (البوليانية).

من ناحية ثانية فإننا نرى أن الحواسيب الاعتيادية هي آلات متوازية عندما ندقق أكثر بالتفاصيل ففي الحقيقة إن كل حاسب مصنوع