إن عملية تقدير وحساب المساحات تعتبر من الأعمال الهامة من أجل تخطيط معظم المنشآت الهندسية هذا و أن المساحات التي يتم حسابها هي المساحات الأفقية، وهناك مصدران أساسيان لتقدير المساحات وهما:
- من المخططات: وهي الأكثر استعمالا لأنها أسعل بالرغم من أنها أقل دقة.
- من الطبيعة: وهي أدق من الحساب على المخطط لانعدام الخطأ التخطيطي ولكن استخدامها ناظر جدا إذ يجب الرجوع إلى المنطقة في الطبيعة لإجراء القياسات للأطوال والزوايا التي نحتاج إليها لحساب المساحات.
وتتوقف دقة نتائج الحساب للمساحات على دقة القياس في الطبيعة، سواء كانت هذه القياسات زوايا أو أطوال أو دقة توقيع الرسم على المخطط والطريقة المتبعة في حساب المساحات. وهناك عدة طرق لإيجاد المساحات ويمكن تقسيم الطرق العامة المستخدمة لإيجاد المساحات إلى الطرق التخطيطية أو الحسابية، الطرق التحليلية، الطرق الميكانيكية.
تتلخص الطرق التخطيطية أو الحسابية بأن تقسم قطعة الأرض المطلوب حساب مساحتها سواء كان ذلك على المخطط أو على الطبيعة إلى أشكال معروفة وبسيطة (مثلثات- مربعات- مستطيلات- أشباه منحرفة) وبحساب مساحة الأشكال البسيطة نتمكن من حساب المساحات الكلية للمنطقة.
ففي الشكل رقم (1) قمنا بتقسيم المنطقة المطلوب حساب مساحتها إلى مربع ومثلثين وبالتالي مساحة المنطقة تساوي إلى مساحة المربع + مساحة المثلثين.
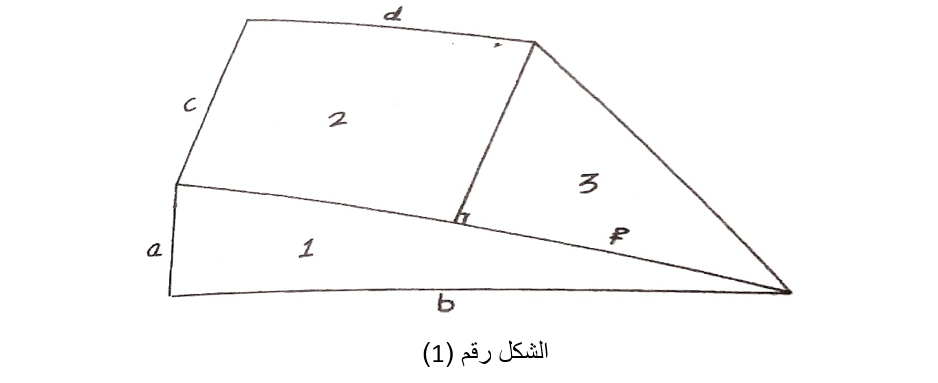
أي أن:
S=S1 + S2 + S3 = ab/2 + cf/2 + c.d
ويلزم عندها إذا كانت عملية القياس تتم على الطبيعة قياس أطوال الأضلاع والأعمدة المنشأة على هذه الأضلاع وذلك بواسطة الشريط والموشور، وإن كانت عملية القياس تتم على المخطط فيجري قياسها بالمسطرة بعد اختزالها إلى مقياس الرسم ومن ثم حساب المساحات.
وإذا كانت بعض حدود قطعة الأرض على شكل منحني كما في الشكل رقم (2) فعندها يتم الحساب كما يلي:
فمثلا إذا كان لدينا السطح ABC المحصور بين المنحني ABC والوتر AC فيمكن أن نعتبر هذا المنحني عبارة عن قطع مكافئ فتكون مساحة الشكل تساوي إلى ثلثي السطح المرسوم على هذا المنحني أي أن:
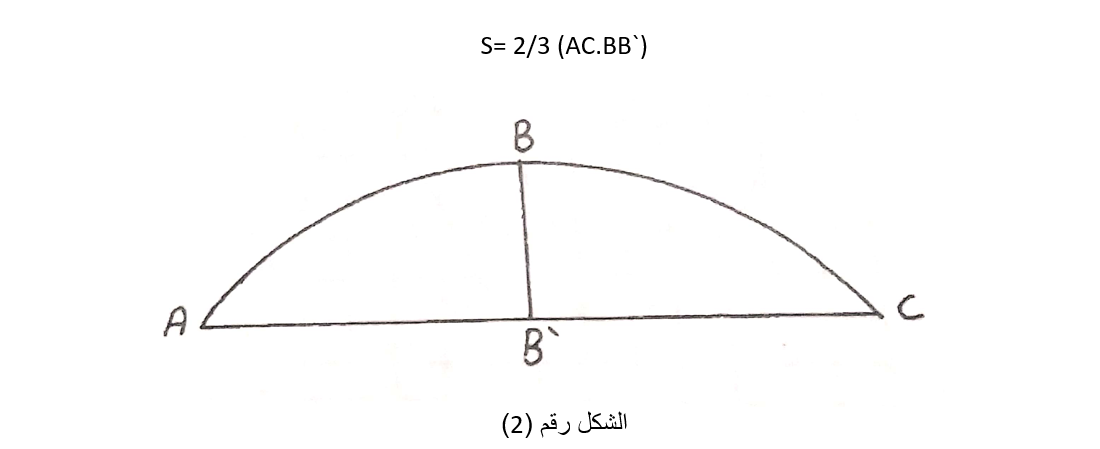
وعندها يلزم قياس المسافة AC والمحور BB` والذي تم إنشاؤه من منتصف الوتر.
يمكن قياس المساحات تخطيطيا وحسابيا بعدة طرق منها:
طريقة شبكة المربعات: وذلك برسم شبكة من المضلعات على ورقة شفافة كورقة الكالك مثلا وطول ضلع المربع 2-5 مم ولقياس مساحة الشكل نقوم بوضع هذه الشبكة على المخطط وعلى المنطقة المطلوب حساب مساحتها كما هو مبين بالشكل رقم (3).
نقوم بحساب عدد المربعات الصغيرة وأجزاء المربعات التي يحصرها الشكل المطلوب حساب مساحته على الشبكة ويتم تقدير الأجزاء كنسبة من المربع وتصبح مساحة الشكل تساوي إلى:![]()
حيث أن S□ مساحة المربع الواحد من الشبكة، n عدد المربعات التي يحصرها الشكل.
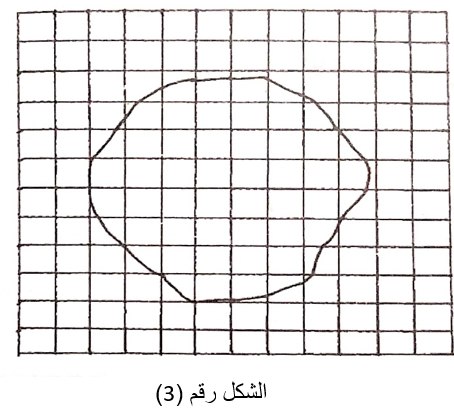
ومن الشكل نجد أن المربعات الصحيحة هو 36 مربعا أما مجموع الأجزاء فهو بحدود 8.5 مربع فيصبح مجموع المربعات التي يحصرها الشكل 44.5 مربعا.
فإذا كان طول ضلع المربع 5 مم ومقياس المخطط 1:1000. فمساحة المربع الصغير لمقياس 1:1000 تساوي إلى 25 متر مربع وعندها تصبح مساحة الشكل:
![]()
طريقة متوسط الارتفاعات: وهذه الطريقة تعد من الطرق التقريبية









