يأخذ المستقيمان في الفراغ ثلاثة أنواع من الأوضاع وهما:
المستقيمان المتوازيان: إذا توازى مستقيمان في الفراغ فمسقطاهما من نفس الاسم متوازيان (الشكل رقم (1)). والعكس الصحيح، إذا توازى كل مسقطين من نفس الاسم لمستقيمين أو توازى مسقطان وانطبق الآخران، أو توازى مسقطان والآخران عبارة عن نقطتين فالمستقيمان متوازيان في الفراغ.
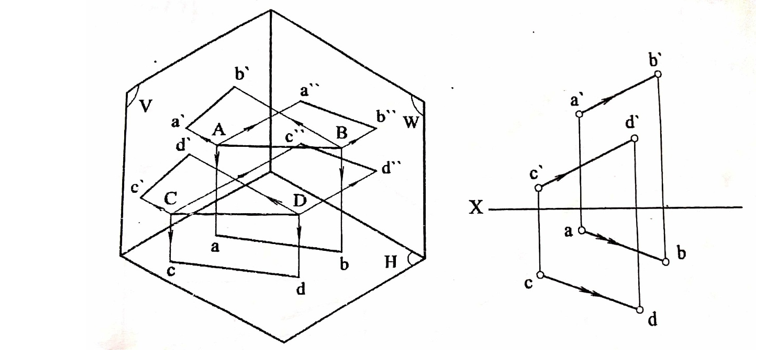
الشكل رقم (1).
المستقيمان المتقاطعان: يكون المستقيمان AB و CD متقاطعين أي يكون لهما نقطة مشتركة عندما تكون نقطة التقاطع m لمسقطيهما الأفقيين ونقطة التقاطع m` لمسقطيهما الجبهيين واقعين على خط تداعي شاقولي واحد، إذ أن النقطة M التي مسقطاها m و m` تمثل نقطة واقعة على كلا المستقيمين المذكورين في نفس الوقت (الشكل رقم (2)).
في الحالة التي تكون فيها إحدى نقاط التقاطع أو كلتاهما خارج حدود الورقة نستخدم مستقيمين يرتكزان على المستقيمين المعطيين، فإذا كان هذان المستقيمان المساعدان متقاطعين فهما واقعان في مستوي واحد والمستقيمان الأصليان يقعان أيضا في هذا المستوي فهما متقاطعان وإلا فهما غير متقاطعين.
في المثال المبين في الشكل رقم (2)، نلاحظ أن المستقيمين المساعدين G1 و G2 غير متقاطعين لأن النقطتين m و n` غير واقعتين على خط تداعي شاقولي واحد وبالتالي المستقيمين AB و CD غير متقاطعين.
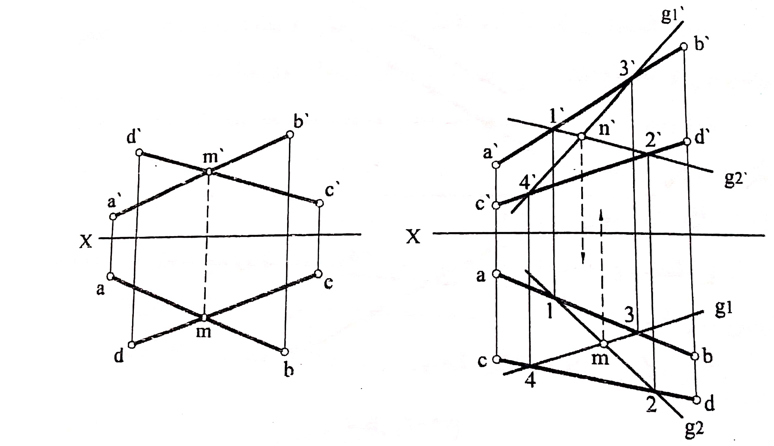
الشكل رقم (2).









