الحالة الإجهادية المستوية 

الحالة الإجهادية المستوية

لدراسة الحالة الإجهادية في نقطة مثل K، الشكل رقم (1)، فإنه يقتطع من حولها عنصر حجمي بشكل متوازي المستطيلات (أو مكعب) أبعاده dz, dy, dx.

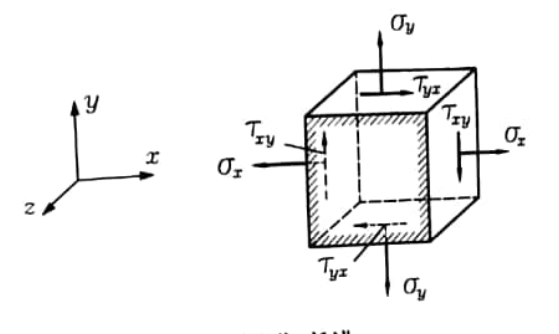
الشكل رقم  (1)

قانون ازدواج الإجهادات المماسية:

إن العنصر الحجمي يجب أن يكون متوازياً، ومن الشكل 1 ، واضح أن القوى الناظمية متوازية، أما القوى المماسية المؤثرة على الوجوه المتقابلة فتشكل مزدوجتين، الشكل1، الأولى r_xy. dy. dz ذات الذراع dxوالثانية : r_yx.dx.dz ذات الذراع dy، وبكتابة معادلة التوازن نجد:

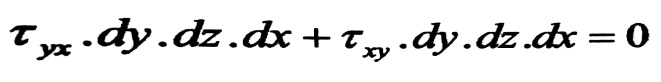
أو

Ꚍ_xy=-Ꚍ_yx→Ꚍ_xy=I Ꚍ_yx I   (1)

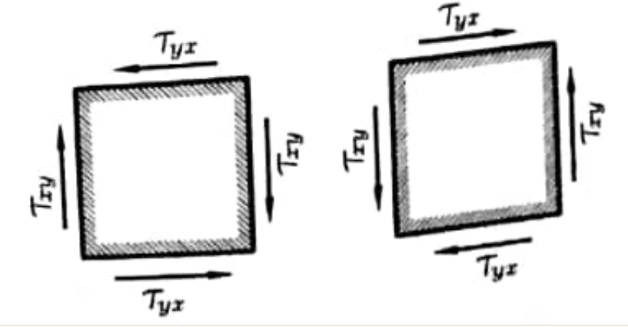
الشكل رقم (2)

إن العلاقة الأخيرة تعد علاقة عامة وتسمى بقانون ازدواج الإجهادات المماسية، أي أن الإجهادات المماسية على سطحين أو ساحتين متعامدتين تكون متساوية بالقيمة المطلقة ويجب أن تكون متجهة بحيث تحاول تدوير العنصر باتجهاين مختلفين، الشكل رقم (2).

الإجهادات على مقاطع مائلة

لنقطع متوازي المستطيلات المبين على الشكل رقم (1) بمستو مائل بزاوية α وعمودي على المستويxoy، وندرس توازن أحد الأجزاء المقطوعة والذي هو عبارة عن الموشور المبين في الشكل رقم (3).

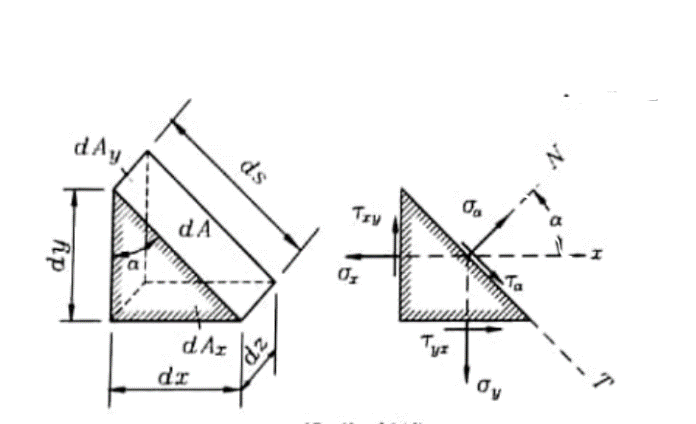
الشكل رقم (3)

ملاحظة:

نعتبر الزاوية α موجبة إذا دار المحور ox بعكس اتجاه عقارب الساعة لينطبق على الناظم N على الساحة المائلة. في الحالة المدروسة (α>0).

لإيجاد الإجهادات الناظمية σ_α  والمماسية r_α الموجودة على المساحة المائلة، نكتب معادلتي التوازن لجميع القوى المؤثرة على وجوه الموشور:

- مساقط القوى على الناظم N على المساحة المائلة يساوي الصفر: