لدراسة آلية هذا التأثير المتبادل سوف نكتفي بأخذ سويتين فقط بعين الاعتبار من مجموعة السويات العديدة الذرات . ولتكن السوية الأولى ذات الطاقة E1 والسوية الثانية E2 .
إن تفاعل الضوء مع الذرات الثلاث يترافق بثلاث عمليات هي : عملية الامتصاص , عملية الإصدار العفوي وعملية الإصدار القسري . وهذه العمليات الثلاث تترافق بانتقالات تحدث في ذرات المادة بين السويتين E1 و E2 عند أي درجة حرارة وهذا ما يتعلق بعملية التوازن الحراري .
سنقوم في هذه المرحلة بدراسة تأثير كل عملية من عمليات الانتقال الثلاث السابقة على معدل التغير في عدد الذرات N2 في السوية المثارة E2 وذلك في حالة التوازن الحراري , فالعلاقة بين عدد الذرات في سويات الطاقة المختلفة عند التوازن الحراري يمكن وصفها بمعادلة ماكسويل بولتزمان التالية :
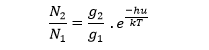
حيث :
k : ثابت بولتزمان .
N2 : عدد الذرات في السوية المثارة E2 .
N1 : عدد الذرات في السوية الأساسية E1 .
g2 و g1 : درجة تعدد السوية الاساسية والمثارة .
T : درجة الحرارة المطلقة .
u : تردد الإشعاع .
h : ثابت بلانك .
الإصدار التلقائي
تعتمد عملية الإصدار التلقائي على عدد الذرات في السوية المثارة N2 فكلما ازداد هذا العدد كلما ساهم ذلك في عملية الإصدار التلقائي كما يتعلق هذا الانتقال بالمعامل A21 الذي يعبر عن احتمال حدوث الإصدار التلقائي ويدعى معامل اينشتاين للإصدار التلقائي , كما أن معدل التغير في عدد الذرات في السوية المثارة بالنسبة للزمن يكون دائما سالبا لأن العدد N2 يتناقص مع الزمن ويمكن التعبير عن ذلك بالمعادلة :
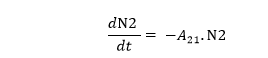
إن هذا الإصدار الذي يزيد من عدد الفوتونات الصادرة يتناسب مع عدد









