تصميم الخوارزميات المتوازية

 *تصميم الخوارزميات المتوازية **

& تعتبر عملية التصميم لخوارزمية معينة أنها عملية حركية حيوية ,و تتميز بعدم وجود قانون أو قاعدة ثابتة للحصول على خوارزمية معينة ذات كلفة قليلة .

و يجدر الذكر أن هناك الكثير من القضايا و المسائل الهامة جداً لم يتم إيجاد خوارزمية لحلها بعد , بحيث تكون ذات كلفة متوسطة أو قليلة  ، و لكن هناك بعض الاستراتيجيات الرئيسية تقود للحصول على خوارزميات ذات كلفة مقبولة.

إن الشكل الطبيعي لتطوير الخوارزميات المتوازية هو بالبدء من الخوارزمية التسلسلية ,و من ثم تحديد الخطوات المستقلة وأخيراً الحصول على الخوارزمية المتوازية , و هذا التحول من التسلسل إلى التوازي ينتج غالباً خوارزميات متوازية ذات كلفة منخفضة.

ومن أجل ذلك تتشأ مسألة تحديد استراتيجيات للحصول على خوارزميات متوازية فعالة, حيث لا يوجد طريقة عامة تعطي أفضل خوارزمية متوازية لمسألة معطاة , و لكن هناك تقانات تستعمل لهذا الغرض و سنعرض بعض هذه الطرائق و التقانات:

سنرمز فيما يلي إلى كل من الزمن والمكونات المادية وعدد المعالجات وللزمن ولعدد المعالجات بآن معا ب: T و H و P و PT على التولي. &

**التقسيم و التخصيص**

& إن الاعتماد الأساسي على هذه التقنية  هو تجزيء المسألة الكبرى إلى مسائل صغيرة جزئية من نفس النوع ولكن بحجم أصغر, ومن ثم إعادة ترتيب وتجميع الحلول.

وهي طريقة فعالة جداً حيث تسمح بتجزئة المسألة إلى مسائل جزئية مستقلة تحل على التوازي وتجمع حلولها للحصول على حل المسالة الأصلية.

أما بالنسبة لكلفة الحل المتوازي لمسألة حسابية من الترتيب n وبالتالي من الحجم H(n) والعمق (T)n لدينا:

لتكن r عدد صحيح يقسم n ولتكن (Hi)n/r و (Ti)n/r (حيث: i=1,2,,,,,r ) هي كلف حل r مسألة جزئية ، ولتكن (Tc)n و (n)Hc هي الكلفة المتوازية الإضافية لحل المسألة الأصلية بعد أن يتم حل المسائل الجزئية. لدينا:

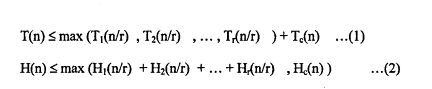
تأتي العلاقة (1) من الحقيقتين التاليتين :

1— استقلالية المسائل .

2- الحاجة لتتفيذ العمل الإضافي عندما تحل المسائل الجزئية فقط. 

تأتي العلاقة (2) من الحقيقتين التاليتين:

1-كل مسألة جزئية تم حلها على التوازي مع الأخريات تحتاج مصادرها المادية الخاصة من  المكونات الصلبة hardware.

2-الكمية الناتجة من المكونات الصلبة هي العدد الأعظمي بين المصادر المطلوبة لحل جميع المسائل الجزئية والمصادر المطلوبة للحصول على الحل الأخير للمسألة الأصلية.

و على افتراض أن جميع المسائل الجزئية متساوية من حيث كلفة التوازي تصبح العلاقتين (1) و (2) كما يلي:

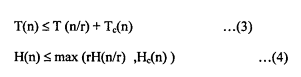
حيث T(n/r) و H(n/r)  هي كلفة المسالة الجزئية من الترتيب n/r .

تعتبر هذه العلاقات من 1 إلى 4 هامة من أجل تحليل الخوارزميات المتوازية التي نحصل عليها من طريقة التقسيم والتخصيص. &

**طريقة استخدام المتجه**

&     طريقة استخدام المتجه Vectorization: تبدأ هذه التقانة من تحليل المسألة و إنتاج الخوارزميات التي تعمل على بنى المعطيات التي تتناسب مع حسابات المتجه (المتجهات والمصفوفات).

وهذه التقانة هامة بشكل خاص في النموذج SIMD  خاصة عندما يكون من المناسب العمل إلى متجه من n ترتيب بالإضافة  إلى n  كمية غير متجهة. &

**تكرار المتجهات**