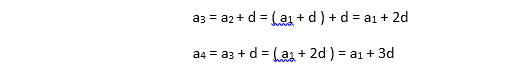يسمى كل تطبيق معرف على مجموعة الأعداد الطبيعية متتالية . إذا أخذ هذا التطبيق قيمة في مجموعة الأعداد الحقيقية سمي متتالية عددية حقيقية ، وإذا أخد قيمة في مجموعة الأعداد العقدية سمي متتالية عددية عقدية ، وفي مجموعة الدوال متتالية دالية ..... وهكذا .
لمجموعة حدود المتتالية قدرة مجموعة الأعداد الطبيعية نفسها ، وذلك لأنه مقابل كل عدد طبيعي يوجد حد واحد في المتتالية هو الحد الذي رقمه هذا العدد الطبيعي ، ومقابل كل حد في المتتالية يوجد عدد طبيعي واحد هو رقم هذا الحد ، ولذلك تكون مجموعة حدود المتتالية غير منتهية دوما بينما تكون مجموعة قيم هذه الحدود منتهية وقد تتألف من قيمة واحدة فقط . نرمز للمتتالية بالرمز
تعريف المتتالية العددية الحقيقية : هي مجموعة لا نهائية من الأعداد الحقيقية المرقمة بواسطة الأعداد الطبيعية x1 , x2 , …… , xn …. ومن الممكن لحدود المتتالية أن تتساوى بالقيمة على الرغم من اختلافها بالأرقام .
المتتالية الحسابية بالخطوة d : تعطى بالعلاقة التراجعية : 
التي تعني أن كل حد في المتتالية ينتج عن سابقه بإضافة العدد الثابت d . أي إذا علمنا قيمة الحد الأول في هذه المتتالية هي a1 فإنه يمكننا حساب قيم جميع الحدود الأخرى حيث : 
Download eMufeed Android Application Now
