الإجهادات والتشوهات في حالة فتل قضيب ذي مقطع دائري  

الإجهادات والتشوهات في حالة قضيب ذي فتل دائري  

لنرسم على المحيط الخارجي لأسطوانة (قبل تعرضها للفتل ) شبكة من الخطوط الطولية الموازية لمحورها (مولدات الأسطوانة) ودوائر مستوياتها عمودية على المحور.

بعد  تأثير عزمي الفتل نلاحظ أن المستطيلات الصغيرة المؤلفة للشبكة المرسومة على السطح الخارجي للأسطوانة تصبح بشكل متوازي أضلاع ، كما أن محورها يبقى مستقيما ، وكذلك الدوائر المحيطية والمستوية قبل الفتل تبقى بدون تغيير بعد الفتل ، وتدور المقاطع العرضية بالنسبة لبعضها البعض بزاوية ما ، الشكل رقم (1).

ونلاحظ أيضا بأن قطر الأسطوانة لا يتغير ، وكذلك المسافة بين المقاطع العرضية لا تتغير ، وهذا يعني أن الألياف الطولية للأسطوانة لا تتطاول ولا تتقاصر ، وبالتالي المقاطع العرضية لا تضغط على بعضها البعض ، أي أن الإجهادات الناظمية معدومة في المقاطع الأسطوانية الطولية و العرضية .

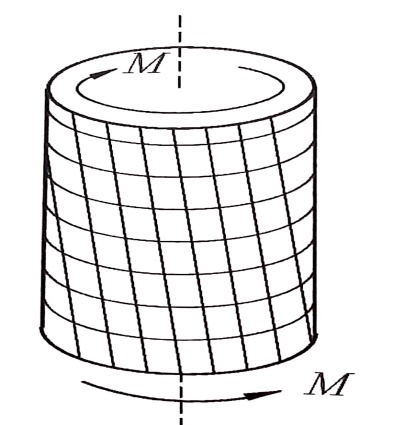
الشكل رقم (1)

- واستنادا لتلك الملاحظات ، ستكون الفرضيات التالية أساسا للاستنتاجات القادمة :

-1 المقاطع العرضية المستوية قبل الفتل تبقى مستوية بعد الفتل (فرضية برنولي ).

-2 أنصاف أقطار المقاطع العرضية تبقى مستقيمة ولا تلتوي أثناء الفتل .

-3 مادة العنصر عند حدوث التشوه يجب أن تبقى ضمن حدود صلاحية قانون هوك .

-4 الأبعاد بين المقاطع العمودية على محور الأسطوانة تبقى متساوية ، وهذا يفسر غياب الإجهادات الناظمية في الاتجاه الطولي .

- وبناء على ذلك فإن فتل قضيب ذي مقطع دائري يمكننا اعتباره نتيجة للانزياح الناتج عن دوران للمقاطع العرضية بالنسبة لبعضها البعض . مما يؤدي إلى ظهور إجهادات مماسية فقط أما الإجهادات الناظمية فتكون معدومة .

ولمعرفة قانون توزع الإجهادات المماسية والتشوهات الحاصلة عن عزوم الفتل ، سندرس قضيبا مقطعه العرضي دائري نصف قطره r ، ومثبت من أحد طرفيه وعلى طرفه الآخر يؤثر عزم الفتل الخارجي M ، الشكل رقم (2) .

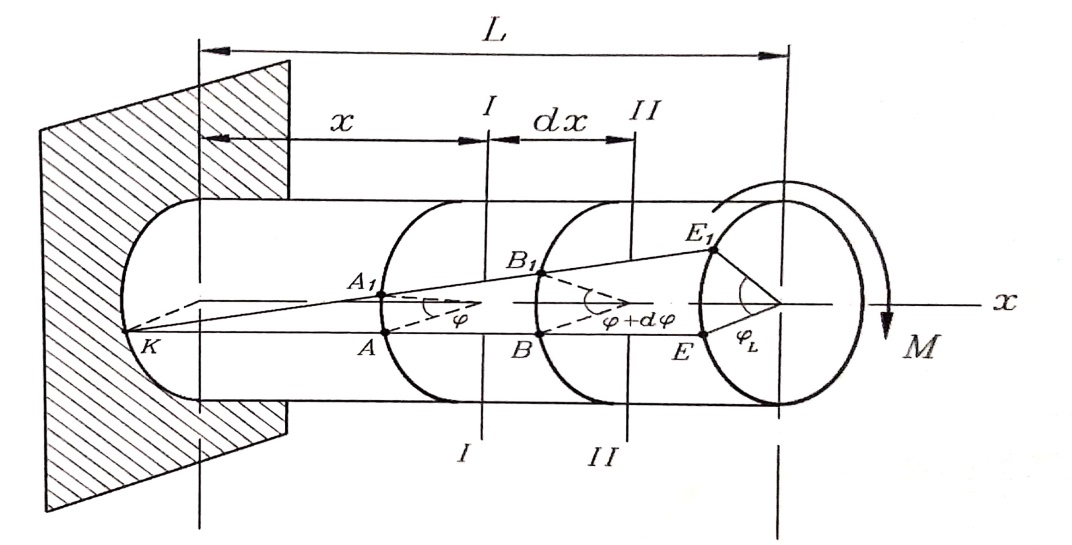
الشكل رقم (2)

سيأخذ المستقيم أو المولد KE بعد الفتل الوضعية KE₁ ، والمقطع I – I الذي يبعد بمقدار x عن الطرف الموثوق سيدور بزاوية ϕ والتي تدعى بزاوية الفتل ، ويدور المقطع المجاور II – II والذي يبعد بمقدار x +dx  يدور بزاوية ϕ + dϕ ، أي أنه يدور بالنسبة للمقطع I – I السابق بزاوية dϕ .

ولندرس بكل منفصل جزء القضيب الذي طوله dx ، ولتبسيط الحل سنفترض أن الطرف الأيسر لهذا العنصر موثوق ، الشكل رقم (3) .

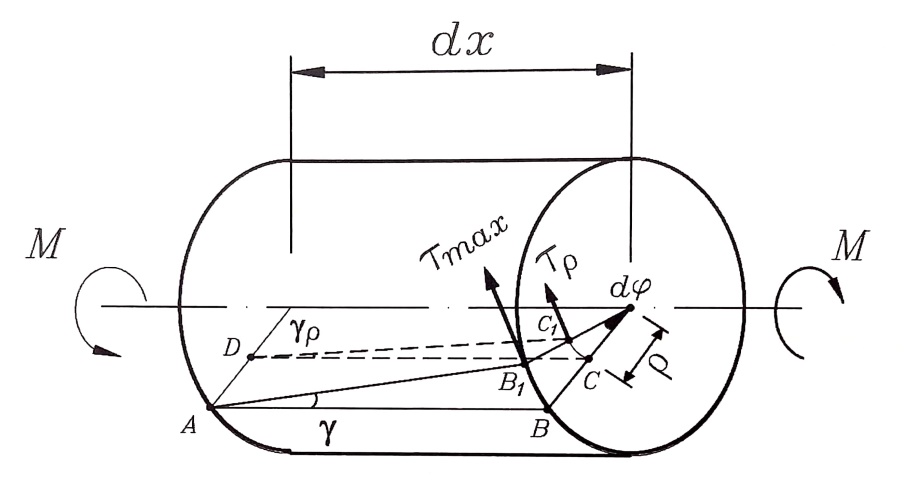
الشكل رقم (3)

إن المولد AB ينتقل إلى الوضعية AB₁ ، إن زاوية القص لهذا المولد ، كما لكافة الألياف الواقعة على سطح القضيب ، هي : y ، ولصغرها ، تعين بالعلاقة :

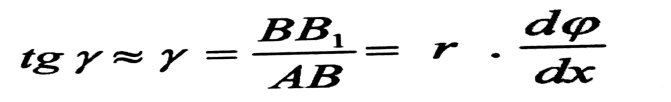
أما بالنسبة للألياف DC التي تبعد بمقدار p عن مركز القضيب :

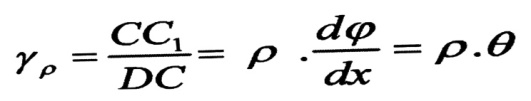
حيث :

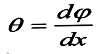  : تسمى يزاوية الفتل النسبية وتقاس بواحدة الزاوية مقسومة على واحدة الطول (deg/m ; deg/cm) أو (rad/m ; rad/cm) .

و من قانون هوك في حالة القص ، يمكن أن نكتب :

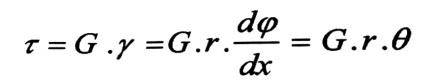  (1)

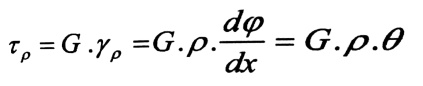       (2)

من هذه العلاقات واضح أن الإجهادات المماسية في نقاط المقطع العرضي تتناسب خطيا مع البعد p لتلك النقاط عن المركز  o . وأن أعظم قيمة للإجهادات المماسية ꚍ_max ستكون في النقاط الواقعة على محيط المقطع العرضي ، أي من أجل : p = r .

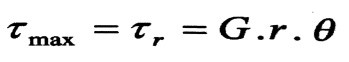
وبهذا نكون قد عينا قانون توزع الإجهادات المماسية ꚍ في مقطع عرضي دائري ، ويبين الشكل رقم (4-b) مخطط توزع الإجهادات المماسية لمقطع حلقي .

أن القيمة 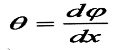الموجودة في العلاقات السابقة يمكن تعيينها من الشرط التالي :