مفهوم مركز الانعطاف
كما ذكرنا سابقا أن الإجهادات المماسية في المقاطع العرضية للقضبان الرقيقة الجدران تحدد بالعلاقة :
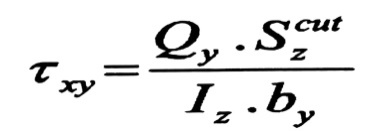
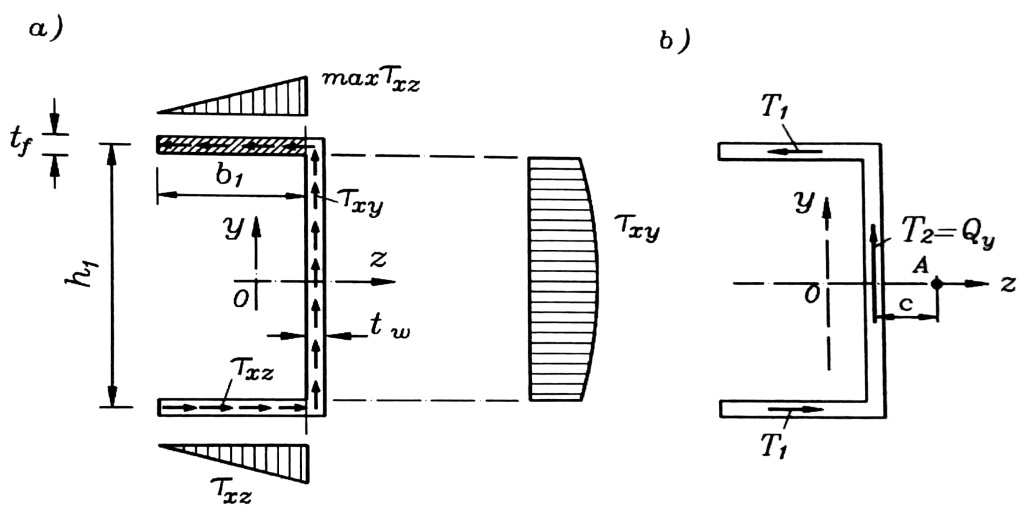
الشكل رقم (1)
وباستخدام الطريقة المشروحة في (مقال حساب الإجهادات المماسية في حالة الانعطاف) يمكننا رسم مخطط الإجهادات المماسية لجائز ذي مقطع ꓛ موثوق من طرف وتؤثر في نهايته الحرة قوة P مطبقة في مركز ثقله .
إن الشكل العام لمخطط توزع الإجهادات ꚍxy و xzꚍ في أي مقطع عرضي ، مبين في الشكل رقم (1-a) .
تظهر على الجسد إجهادات مماسية ꚍxy ، وتظهر محصلتها كقوة قاصة قيمتها T2 ، الشكل رقم (1-b) ، إذا أهملنا الإجهادات المماسية ꚍxy في الجناحين ، فإنه يمكننا كتابة المساواة التقريبية :
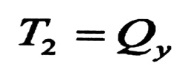
في الجناحين تظهر إجهادات مماسية ꚍxy ذات اتجاه أفقي قيمتها الأعظمية max ꚍxz تعين بالعلاقة :
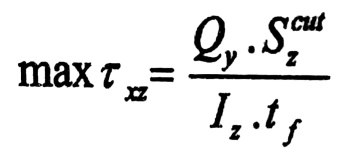
حيث :
Szcut : العزم الستاتيكي لمساحة الجناح بالنسبة للمحور المحايد oz .
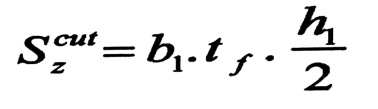
وهكذا فإن :
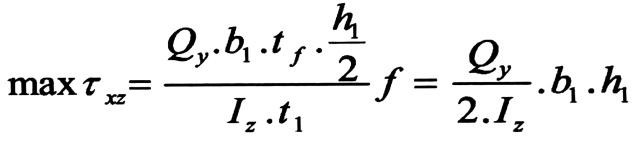
إن محصلة القوى القاصة في الجناح ، عبارة عن مساحة مخطط الإجهادات المماسية مضروبا بسماكة الجناح ، أي :
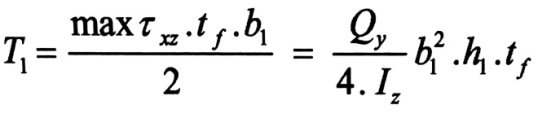 (1)
(1)
في الجناح السفلي توجد أيضا نفس القوى القاصة في الجناح العلوي ، لكن تعاكسها بالاتجاه ، فالقوتان T1 تشكلان مزدوجة عزمها :
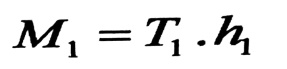 (2)
(2)
- وهكذا نتيجة الإجهادات المماسية ꚍxy و xzꚍ تظهر ثلاث قوى مماسية داخلية ،تظهر على الشكل رقم (1-b) ،والذي نلاحظ عليه أن القوتين T1 و T2 تسعيان إلى تدوير المقطع العرضي حول مركز ثقله بنفس الاتجاه .
- إذن في المقطع المجرى ꓛ سيظهر عزم فتل داخلي يتجه عكس دوران عقارب الساعة ، وهكذا عند انعطاف جائز ذي مقطع عرضي على شكل مجرى ، محمل بقوة مركزة P في مركز ثقل مقطعه العرضي ، فإن الجائز يتعرض لعزم فتل في نفس الوقت .
إن القوى المماسية الثلاثة يمكن استبدالها بقوة رئيسية وعزم رئيسي ، قيمة هذا العزم تتعلق بموضع النقطة الذي تم فيه تركيز القوة ، ومن الممكن اختيار مثل تلك النقطة A التي ينعدم بالنسبة لها العزم الرئيسي ، هذه النقطة تسمى مركز الانعطاف ، وذلك بمساواة عزم القوى القاصة بالصفر :
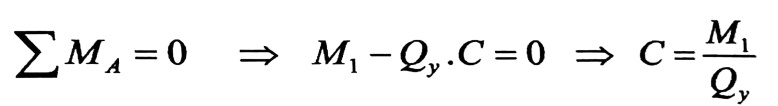
حيث :
C : البعد بين محور الجسد ومركز الانعطاف .
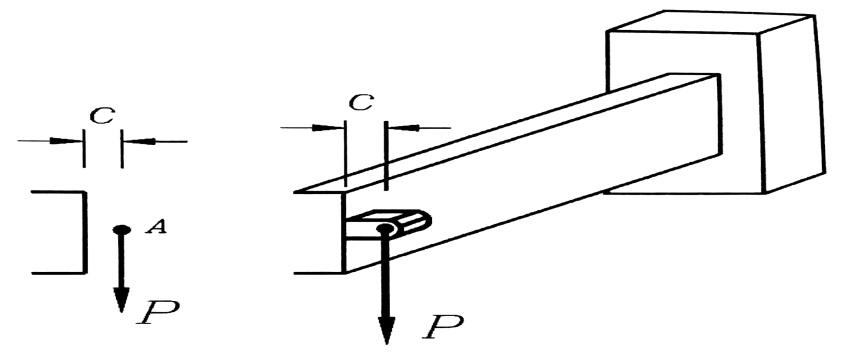
الشكل رقم (2)
وإذا أخذنا العلاقتين رقم (1) و (2) بعين الاعتبار ، فإن بعد مركز الانعطاف عن محور الجسد سيعين بالعلاقة :
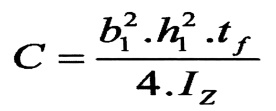 (3)
(3)
- كما أن العنصر المبين بالشكل رقم (2) ، يقاوم تشوهات الفتل بشكل سيء . وتجنبا لذلك عند استعماله









