الجوائز غير المقررة ستاتيكيا والمستندة على قاعدة مرنة
إن الجائز المحمل بحمولة ما يجب أن يثبت بشكل لا ينزاح فيه كجسم صلب. في حال تأثير الحمولة في مستو واحد ، فإن عدد الأربطة اللازمة لتثبيت جائز هي ثلاثة ، ونعتبر هذه الأربطة الثلاثة ضرورية بشكل مطلق ، إذا لو أبعدنا أحدها يصبح الجائز مجموعة غير مستقرة هندسيا (أي يحصل ما يسمى بالميكانيزم) ، وفي مثل هذه المجموعة سيحصل انتقالات للنقاط دون حدوث تشوهات في قضبان المجموعة .
وباعتبار أنه يمكن تشكيل ثلاث معادلات توازن لمجموعة قوى مستوية مؤثرة في جائز ، فإن رد أفعال الأربطة يمكن إيجادها فقط من معادلات التوازن ، ويعتبر الجائز المثبت بمثل تلك الأربطة جائزا مقررا ستاتيكيا .
ويمكن عمليا مشاهدة جوائز يكون فيها عدد الأربطة أكثر من العدد اللازم لتأمين الاستقرار الهندسي ، أي بعض الأربطة سيكون زائدا ، وتسمى مثل هذه الجوائز بالجوائز غير المقررة استاتيكيا ، إذ لا نستطيع تحديد ردود الأفعال من معادلات التوازن .
إن تعبير (الأربطة الزائدة) تعبير شرطي ، حيث تكون ضرورية حسب ظروف عمل المنشأ ، فبدونها يمكن أن يفقد الجائز متانته وصلابته .
في الشكل رقم (1) نشاهد جائزين لهما نفس الطول ومحملين بنفس الحمولة ، إن قيمة السهم في الجائز المقرر استاتيكيا ، الشكل رقم (1-a) ، أكبر بكثير منها في الجائز غير المقرر استاتيكيا ،وبهذا فالرابطان الإضافيان جعلا الجائز أكثر صلابة .
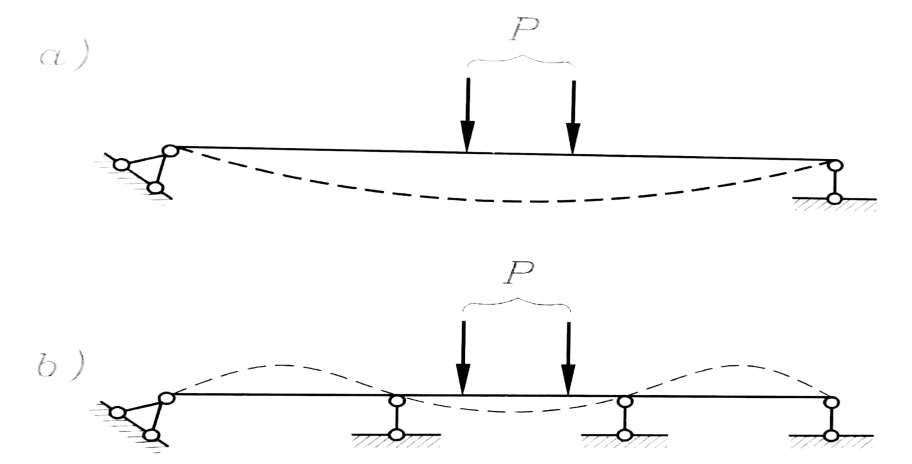
الشكل رقم (1)
إن عدد ردود الأفعال في الجوائز غير المقررة استاتيكيا هو دائما أكثر من عدد معادلات التوازن ، والعدد الزائد عن ثلاثة يمثل درجة عدم التقرير الستاتيكي .
في الشكل رقم (2) نشاهد جائزين لكل منهما أربعة ردود أفعال ، وباعتبار عدد معادلات التوازن المستقلة ثلاثة ، فالجائزان إذن غير مقررين من الدرجة الأولى .
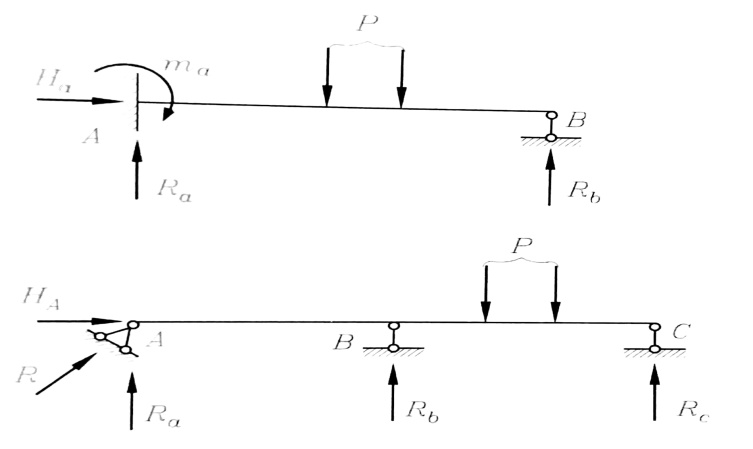
الشكل رقم (2)
أما كلا من الجائزين المبينين في الشكل رقم (3) فهو غير مقرر من الدرجة الثانية .
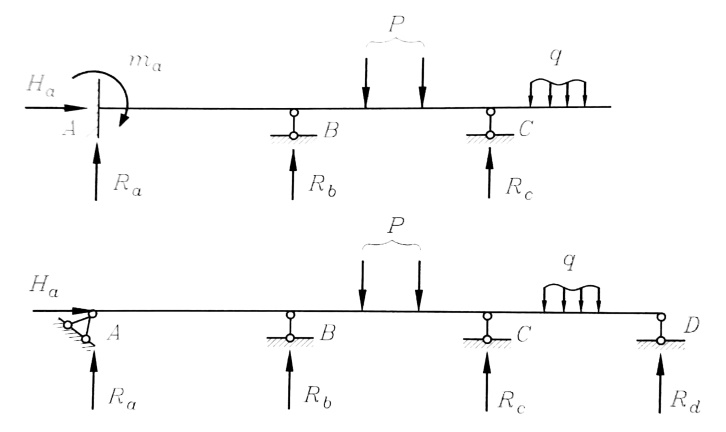
الشكل رقم (3)
إن طريقة حساب الجوائز غير المقررة استاتيكيا ، لا تختلف كثيرا عن الطرق المستخدمة في المسائل غير المقررة استاتيكيا في الشد والفتل . ففي البداية نهمل الروابط الزائدة ونستعيض عنها بردود أفعال مجهولة ، أي يتحول الجائز المعطى إلى جائز مقرر استاتيكيا ، ويسمى عندئذ بالجائز الرئيسي .
ولتحديد قيم المجاهيل الزائدة Ra , Rb , ……Rn نشكل شروط تشوه المجموعة بحيث تتطابق تشوهات المجموعة الرئيسية تحت تأثير الحمولات المطبقة والمجاهيل الزائدة ، مع تشوهات المجموعة الأصلية غير المقررة استاتيكيا ، وعن شروط تشوهات المجموعة ستنتج مجموعة معادلات نسميها معادلات التشوه .
وبعد حساب المجاهيل الزائدة نوجد ردود الأفعال المتبقية من معادلات التوازن ، ومن ثم نرسم مخططات القوى الداخلية .
إن المجموعة الرئيسية يمكن اختيارها بأشكال مختلفة من أجل نفس الجائز ، وبالتالي معادلات التشوه سوف تختلف ، الشكل رقم (4) ، فمثلا من أجل المجموعة رقم (4-b) ، فمثلا من أجل المجموعة رقم (4-b) تأخذ معادلتا التشوه الشكل التالي :









