السهوم في الانعطاف المائل
بتحليل القوة P إلى مركبتين Px , Py ، الشكل رقم (1) نوجد ، وبشكل منفصل ، السهم الناتج عن كل مركبة على حدة ، لنرمز للسهم في نهاية الجائز الظفري الذي طوله L ، وفق اتجاه المحورين الإحداثيين y , z بالرمز fy , fz .
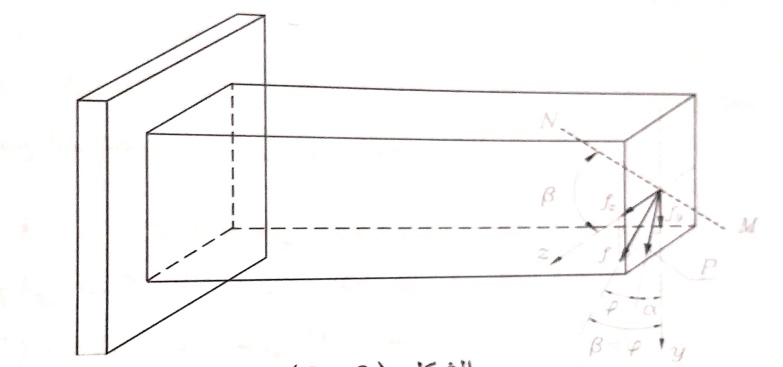
الشكل رقم (1)
ونعلم سابقا أن :
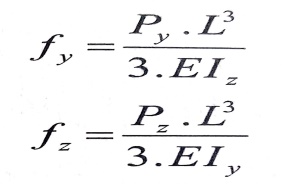
لذلك فإن السهم الكلي سيكون عبارة عن المجموع الهندسي للسهمين fy , fz :
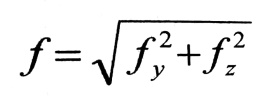
ولمعرفة اتجاه محصلة الانتقالات (السهم) نعين زاوية ميل تلك المحصلة بالنسبة للشاقول :
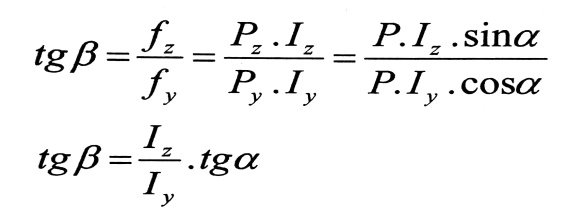(1)
بمقارنة العلاقة رقم (1) مع العلاقة رقم (3) من مقال (تحديد موضع المحور المحايد في مقطع عرضي لجائز في حالة الانعطاف المائل ) ، نجد أن : β = ϕ .
- أي أن اتجاه السهم عمودي على المحور المحايد . ومن هنا نستنتج الشرط الهام التالي وهو أن السهم لا يتطابق مع اتجاه الحمولة المؤثرة بل يميل عليه ، وهذا سبب تسمية الانعطاف بأنه مائل .
إذا كانت الحمولة عبارة عن مجموعة من القوى في مستو واحد ، فإن محور الجائز المنعطف سيقع في مستو آخر لا يتطابق معه ، في الحالات التي تؤثر فيها مجموعة من القوى الفراغية التي لا تقع في مستو واحد ، فغن محور الجائز المنعطف سيكون عبارة عن منحن فراغي .
مثال :
عين القيمة الأعظمية للإجهادات الناظمية σmax والسهم الأعظمي الكلي f للجائز الخشبي المبين بالشكل رقم (2) ، علما أن مقطعه العرضي مستطيل أبعاده cm(15 x 20) .
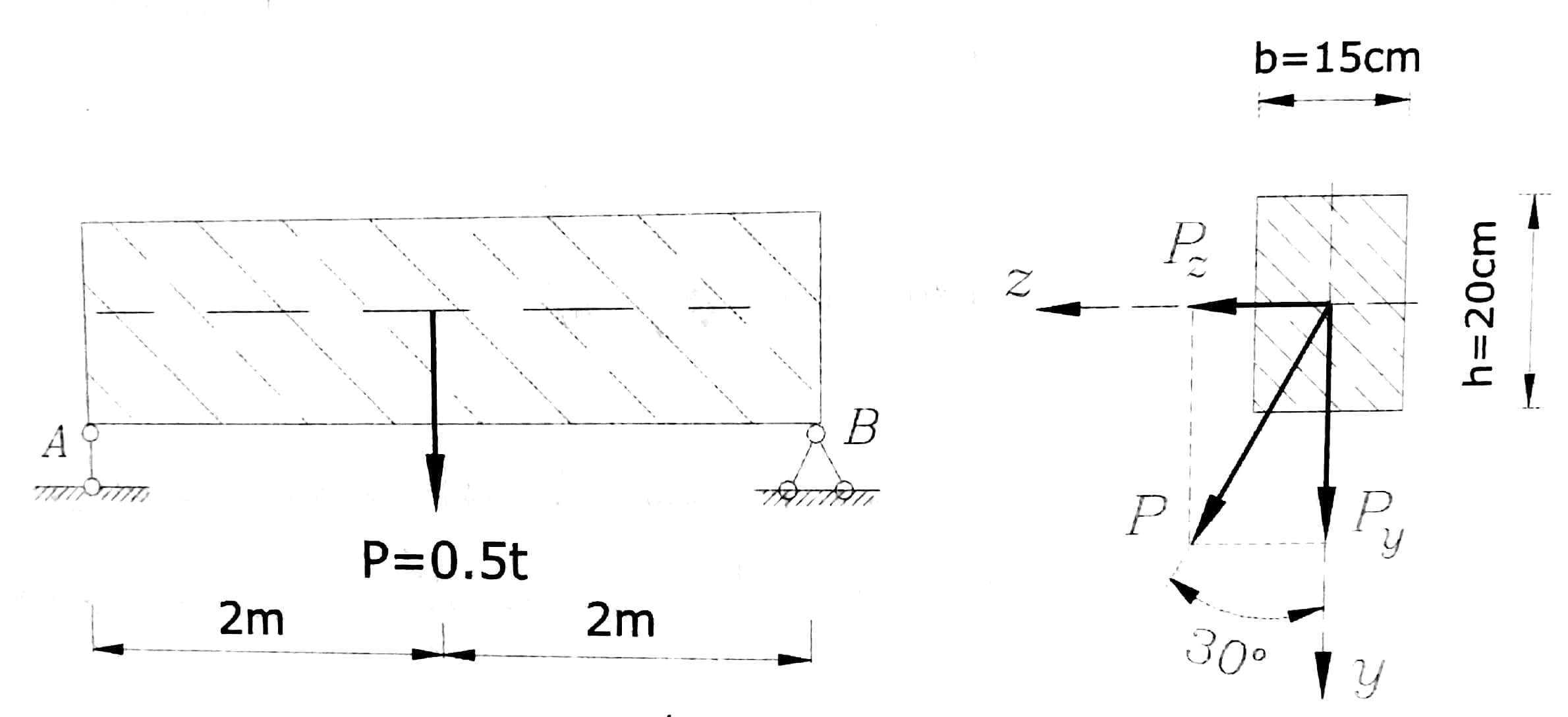
الشكل رقم (2)
الحل :
نحلل القوة P إلى مركبتين : أفقية Pz تولد عزما My وشاقولية Py تولد عزما Mz .
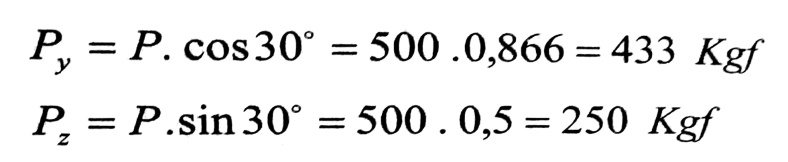
ويكون عزم الانعطاف في المستوي الشاقولي أعظميا في منتصف الجائز وقيمته تساوي :
وكذلك يكون أعظميا في المستوي الأفقي عند المقطع نفسه :
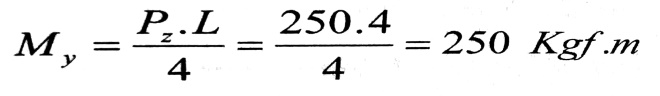
نعين العزمين المقاومين Wz , Wy لمقطع الجائز المعطى :
قم بتنزيل تطبيق eMufeed Android الآن
