تعيين الإزاحات بطريقة الجائز المرافق (الطريقة التحليلية التخطيطية) 

   تعيين الإزاحات بطريقة الجائز المرافق (الطريقة التحليلية التخطيطية)

تعد الطريقة التحليلية – التخطيطية طريقة عملية لدراسة التشوهات (الانتقالات – زوايا الدوران) في الجوائز وخاصة في الحالات التي يطلب فيها تعيين التشوهات في مقطع واحد أو في مقاطع محددة من الجائز .

وبما أن علاقة عزم الانعطاف M_Z بالحمولة الموزعة q هي :

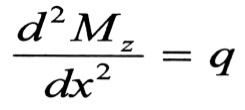
والمعادلة التفاضلية للخط المرن (محور الجائز المنحني ) هي :

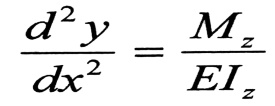
نلاحظ وجود تشابه بين هاتين العلاقتين ، لذلك فمسألة تعيين الانتقالات يمكن تحويلها إلى مسألة تعيين العزوم الناتجة عن حمولة وهمية تسمى بالحمولة المرنة ، مؤثرة على جائز وهمي يدعى بالجائز المرافق ، وقيمتها :

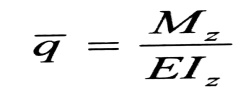
فالعزم الناتج عن تلك الحمولة M ، يساوي السهم y الناتج عن الحمولة الحقيقية المؤثرة في الجائز الحقيقي ، وحيث أن :

يمكن القول بأن زاوية الدوران في الجائز الحقيقي المعطى ، تساوي عدديا القوة القاصة في الجائز المرافق ، أي :

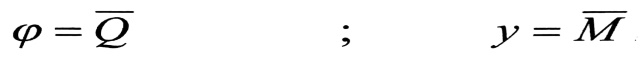
- إن هاتين العلاقتين يجب أن تراعيان في جميع نقاط الجائزين المعطى والمرافق .

باختصار يمكن القول إن مخطط السهم وزاوية الدوران في الجائز المعطى ، يجب أن يتطابقا بشكل تام مع مخططي Q و M للجائز المرافق ، من حيث الإشارة وقيمة إحداثيات كلا المخططين .

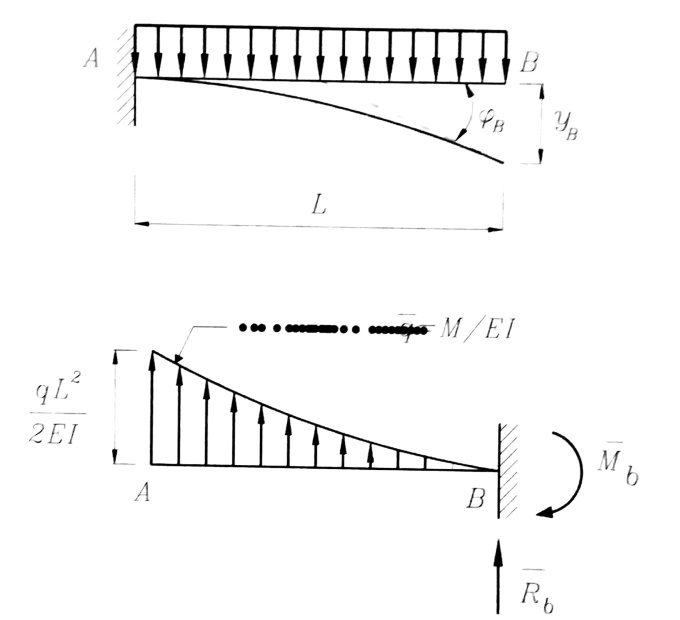
لإنجاز هذا يتطلب أن يكون هناك تشابه تام في الشروط الطرفية لكلا الجائزين ، وكمثال على هذا ندرس الجائز الظفري الموثوق من طرفه الأيسر .

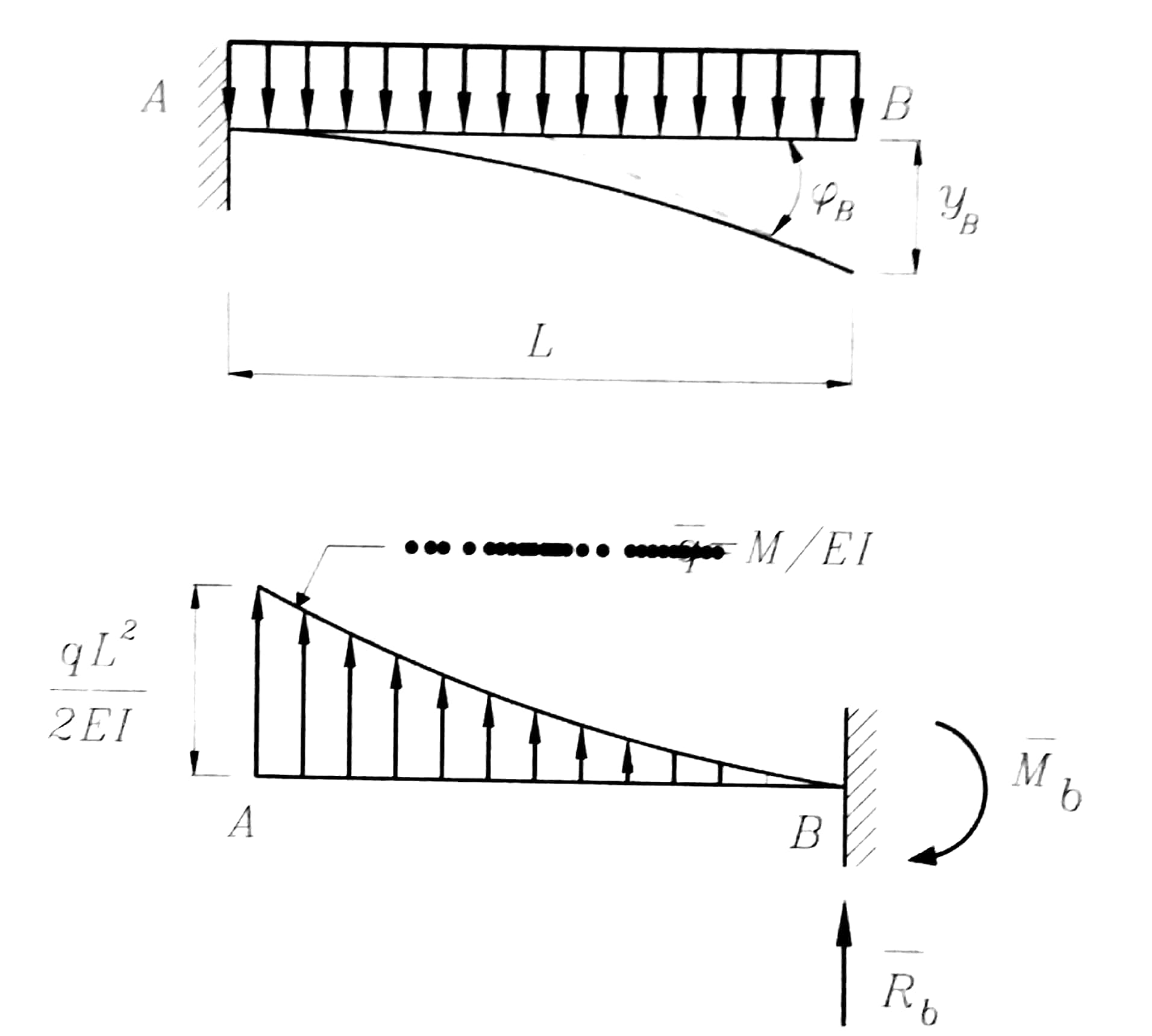
الشكل رقم (1)

- من الشكل نلاحظ أن :

-1 زاوية الدوران والسهم في النقطة A من الجائز الحقيقي يساويان الصفر (المسند الموثوق) .

-2 زاوية الدوران والسهم في النقطة B من الجائز الحقيقي ليسا صفرا بالضرورة (النقطة B حرة ) .

- ومنه نستطيع القول أنه بالنسبة للجائز المرافق ذي الحمولة المرنة :

أ- يجب أن يكون القص والعزم في النقطة A مساويين للصفر ، وبالتالي فالنقطة A حرة .

ب- إن القص والعزم في النقطة B ليسا صفرا بالضرورة ، وبالتالي النقطة B موثوقة .

- وبشكل عام يمكن القول :

المسند الموثوق في الجائز الحقيقي يقابله نهاية حرة في الجائز المرافق ، والعكس بالعكس .

وإذا أخذنا الجائز المستمر المبين في الشكل رقم (2) ، فنلاحظ ما يلي :

الشكل رقم (2)

-1 نظرا للاستمرارية فإن زاوية الدوران تكون واحدة على جانبي المسند في الجائز الحقيقي ، وبعبارة أخرى لا يمكن رسم أكثر من مماس واحد لنقطة المسند .

-2 إن السهم عند المسند يساوي الصفر (لا يحدث هبوط في الأساسات ).

- فتكون الحالة في الجائز المرافق الشكل رقم (1-b) كما يلي :

أ- يجب ألا يحدث تغير مفاجئ في القص عند النقاط A و B .

ب- يجب أن يكون العزم مساويا للصفر عند النقاط A و B .

إن الشيء الوحيد الذي يحقق هذين الشرطين هو أن تكون النقاط A و B في الجائز المرافق مفصلا .

وبصورة عامة ، إن المسند الداخلي للجائز الحقيقي يقابله مفصل في الجائز المرافق .

والجدول رقم (1) يبين شروط المساند في الجوائز المرافقة :

الجدول رقم (1).