تأثير عزمي انعطاف وفتل بنفس الوقت على جائز مقطعه العرضي دائري
غالبا ما نصادف في الحياة العملية في حال جائز مقطعه العرضي دائري تعرضه لعزمي فتل وانعطاف في وقت واحد . فالقوى التي تنتقل إلى المحور الدوراني عن طريق البكرة أو دولاب تنظيم السرعة ، يمكن أن تؤدي إلى عزم فتل وعزم انعطاف .
لدينا الحالة البسيطة التالية على الشكل رقم (1) .
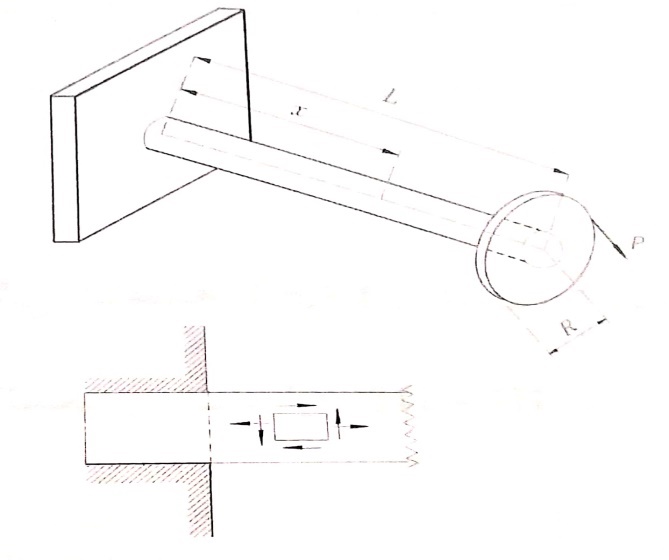
الشكل رقم (1)
فالقضيب الدائري موثوق من إحدى نهايتيه ومحمل بالطرف الآخر بقوة شاقولية P مطبقة على مسافة R من محوره .
يمكن الاستعاضة عن هذه الحالة بتحميل القضيب بعزم فتل : Mt = P.R ، وقوة عرضية P يؤثران في النهاية الحرة من القضيب .
يعتبر عزم الفتل ثابتا على طول المحور ، أما عزم الانعطاف الذي تسببه القوة P في أي مقطع فيعطى بالعلاقة :
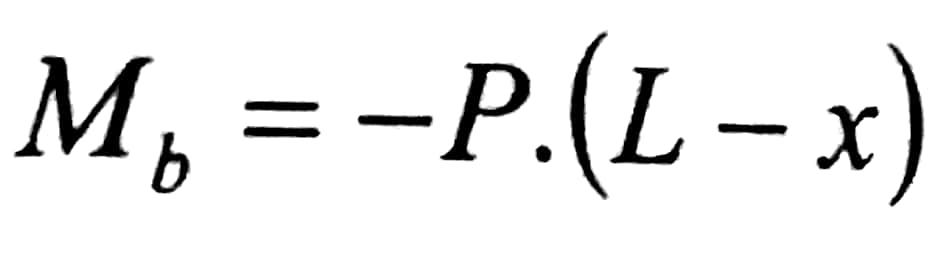 (a)
(a)
- عند البحث عن الإجهادات الأعظمية التي تظهر في القضيب ، يجب ملاحظة ما يلي :
-1 الإجهادات المماسية الناتجة عن عزم الفتل Mt .
-2 الإجهادات النظامية الناتجة عن عزم الانعطاف Mb .
-3 الإجهادات المماسية الناتجة عن القوة القاصة Q = P .
إن الإجهادات المماسية الأعظمية الناتجة عن عزم الفتل تظهر على سطح القضيب ، وتعطى قيمتها بالعلاقة :
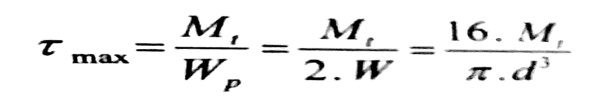 (b)
(b)
أما الإجهادات الناظمية الأعظمية σx الناتجة عن عزم الانعطاف Mb ، فتكون في الألياف الأبعد عن المحور المحايد عند النهاية الموثوقة ، حيث يكون عزم الانعطاف أعظم ما يمكن عدديا وتعطى قيمة الإجهادات بالعلاقة :
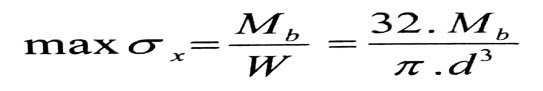 (c)
(c)
أما الإجهادات المماسية الناتجة عن تأثير القوة القاصة فتملك في الواقع أهمية ثانوية ، لأن قيمتها العظمى تكون عند المحور المحايد حيث تنعدم الإجهادات الناظمية الناتجة عن عزم الانعطاف لذا تكون الإجهادات المركبة الأعظمية عادة في تلك النقاط التي تكون فيها الإجهادات (1) و (2) أعظمية ، ففي حالتنا هذه تكون في الألياف على السطح العلوي والسفلي عند نهاية القضيب الموثوقة .
ويظهر الشكل رقم (1) الإجهادات المؤثرة على عنصر واقع في الجزء العلوي للنهاية الموثوقة من القضيب . ونوجد الإجهادات الرئيسية لهذا العنصر بالعلاقات :
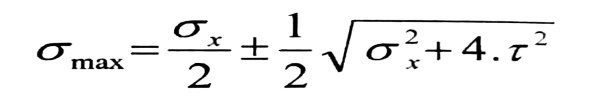
وباستعمال العلاقتين (b) و (c) ، نجد :
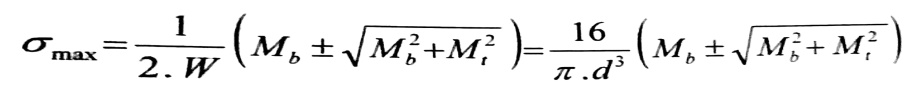 (1)
(1)
من العلاقة رقم (1) نلاحظ σmax,min لهما نفس القيمة كما في حالة الانعطاف البسيط لقضيب يؤثر عليه عزم انعطاف مكافئ يساوي :
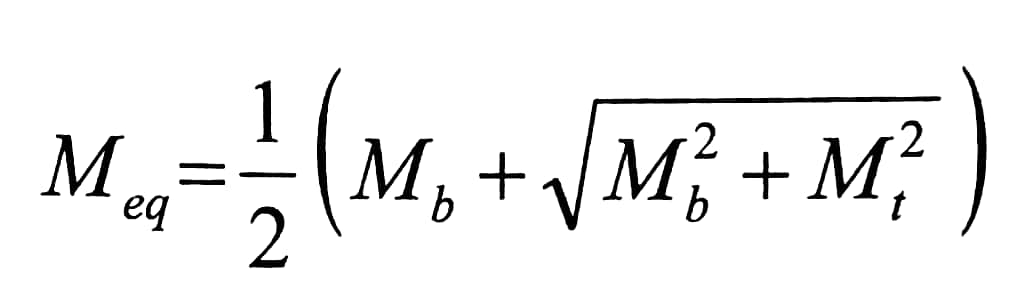
وتعطى الإجهادات المماسية الأعظمية بالعلاقة :
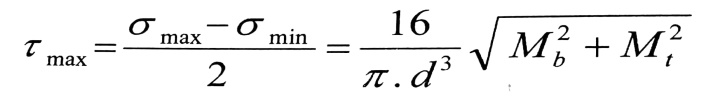 (2)
(2)
في التطبيقات العملية ، ومن أجل تعيين القطر الأمين لقضيب مصنوع من مادة لينة ، نستعمل عادة نظرية الإجهادات المماسية الأعظمية (النظرية الثالثة في المتانة) ونرمز للإجهادات المسموحة على القص بالرمز [ꚍ] ، وبتعويضها بدلا من ꚍmax في العلاقة رقم (2) نوجد العلاقة التالية التي تحدد قطر القضيب :
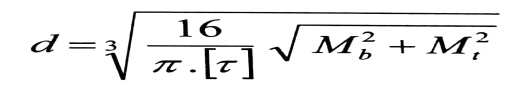 (3)
(3)
إن المناقشة السابقة كانت لقضيب دائري مصمت ، أما بالنسبة لقضيب حلقي قطره الخارجي d والداخلي d1 ، فإن :
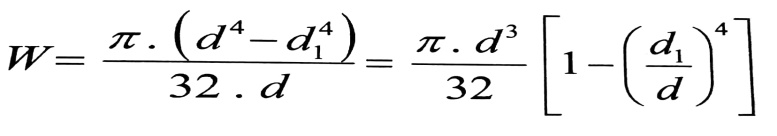
وبفرض أن d1/d = n ، وبالتعويض في العلاقة رقم (1) ، نجد :
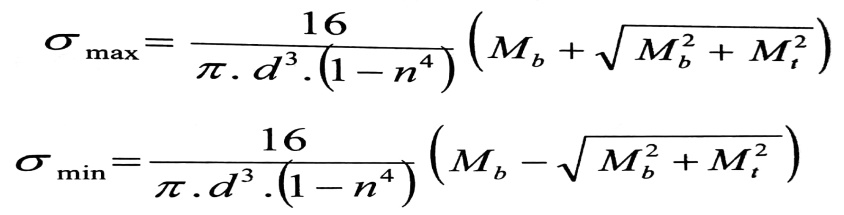 (4)
(4)
وتكون الإجهادات المماسية الأعظمية :
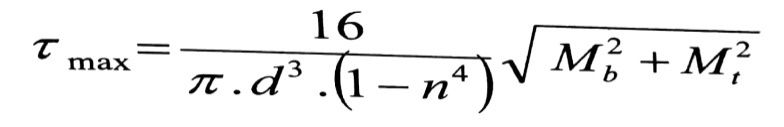 (5)
(5)
وعندئذ سيكون :









