تأثير عزم الانعطاف والقوى المحورية في آن واحد
كثير من عناصر المنشآت تعمل في وقت واحد على الانعطاف والشد أو الضغط ، وكحالة بسيطة نبحث في عمود تؤثر عليه حمولة تسبب في أي مقطع عرضي عزم انعطاف وقوة قاصة ، الشكل رقم (1-a) . بفرض أن للعمود صلابة كبيرة يمكن إهمال تشوهاته ، وعدم الأخذ بعين الاعتبار عزوم الانعطاف الناتجة عن القوة P ، وبفرض أن مقطع العمود لا ينزاح أفقيا فيمكن قبول مبدأ (استقلالية تأثير القوى) وتحدد الإجهادات في نقطة C كمجموع إجهادات ناتجة عن الضغط والانعطاف .
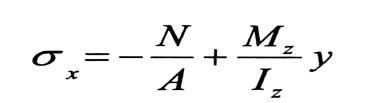
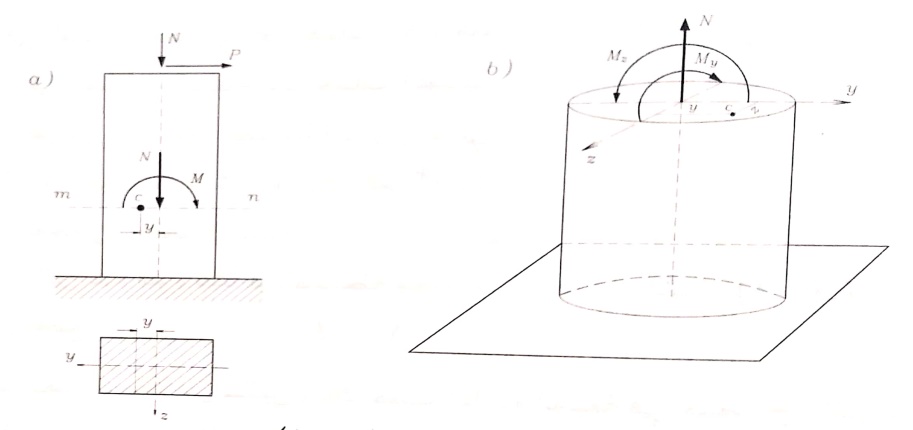
الشكل رقم (1)
إذا كانت الحمولة ستسبب عزوما بالنسبة لمحوري العطالة الرئيسين ، الشكل رقم (1-b) ، فإن الإجهادات الناظمية ستحدد كمجموع ثلاثة إجهادات :
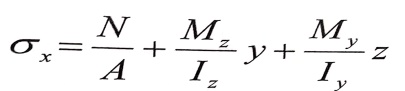 (1)
(1)
باستخدام هذه العلاقة يمكن تحديد الإجهادات في أي نقطة وإيجاد الإجهادات الأعظمية في المقطع العرضي المعطى . إذا كان للمقطع العرضي للجائز شكل بسيط كمستطيل أو مقطع I ، فلتحديد الإجهادات الأعظمية يجب حساب الإجهادات في مجموعة من النقاط المميزة التي يمكن تحديدها ، أما إذا كان للمقطع شكل معقد ، فإننا نعين أولا موضع المحور المحايد ثم نبدأ بالبحث عن أبعد نقطة عن ذلك المحور والتي ستكون فيها الإجهادات أعظمية .
تأثير لا مركزية القوة المحورية :
تحديد الإجهادات : نبحث في مسألة تحديد الإجهادات في عمود كتلي معرض لضغط لا مركزي ، الشكل رقم (2) ، مثل هذه الحالة نشاهدها عادة في المنشآت الجسرية عند حساب ركائزها ، وكذلك في المنشآت السكنية عند حساب أعمدتها ، نفترض أن القوة الضاغطة تؤثر في النقطة C ذات الإحداثيات zp , yp المأخوذة بالنسبة لمحاور العطالة الرئيسية .
ونتيجة تأثير هذه القوة تنشأ قوة ضاغطة محورية في أي مقطع عرضي : N = ‒ P .
وعزما انعطاف سيكونان سالبين وذلك حسب القاعدة المتبعة في اصطلاح الإشارات ، حيث أنهما يسببان ضغطا في النقاط الواقعة في الربع الأول (الموجب) .
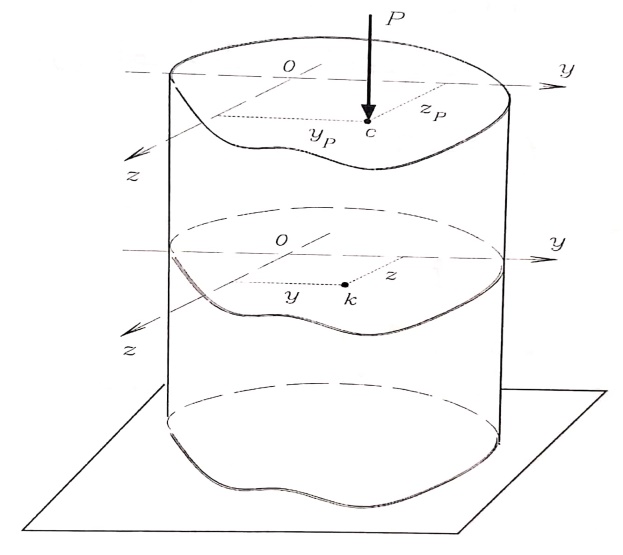
الشكل رقم (2)
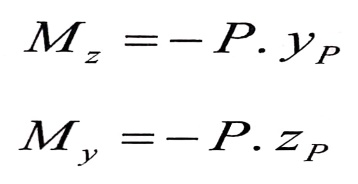
تعطى الإجهادات في نقطة ما (K) تقع في الربع الموجب لمقطع عرضي اختياري ما بالعلاقة :
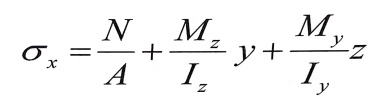 (2)
(2)
بواسطة هذه العلاقة نستطيع أن نحدد الإجهادات في أي نقطة من العمود المضغوط ، حسب إحداثياتها الجبرية y,z .
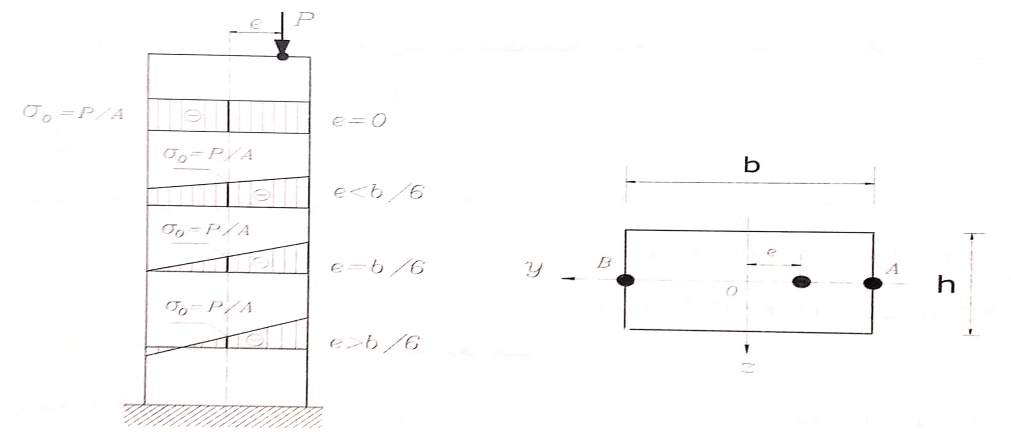
ندرس حالة خاصة من الضغط اللامركزي لعمود مقطعه العرضي مستطيل ، عندما تقع القوة على أحد محاور العطالة الرئيسية ونفرض أنها تقع على المحور (oy) (zp = 0 , yp = e) ، الشكل رقم (3) . بالتعويض في العلاقة رقم (2) ، ومن أجل الألياف الطرفية نجد :
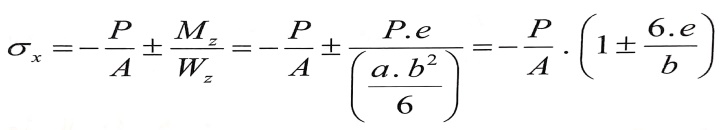
الشكل رقم (3)
من هذه العلاقة نرى ما يلي : عندما تكون e = 0 ، فإن الإجهادات في نقاط المقطع العرضي تكون متساوية وتساوي : σ0 = P/A .
- عندما : e < b/6 ، تكون للإجهادات في كافة نقاط المقطع العرضي إشارة واحدة (ضغط) .
- عندما : e = b /6 ، تكون الإجهادات في النقطتين A , B ، هي :
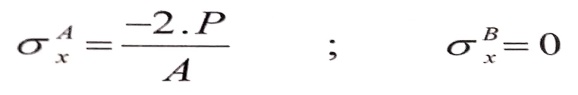
- عندما e > b/6 ، فالمحور المحايد يقع داخل المقطع ويقسمه إلى قسمين ،









