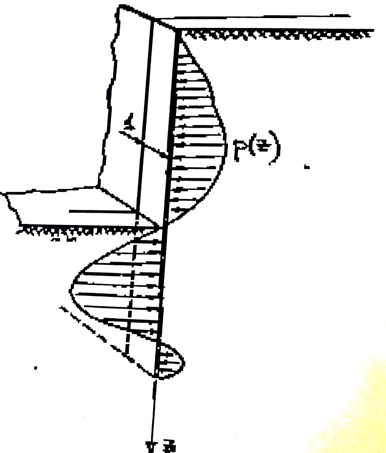
بشكل عام يمكن أن يشبه حساب الصفيحة الوتدية بحساب جائز مستقيم، وذلك بأخذ واحدة العرض من الصفيحة الخاضعة لحمولة موزعة P(z) على كامل الطول، الشكل رقم (3).
وهذا لا يعني بأننا نقبل بشكل أتوماتيكي أن فعل ورد فعل التربة لهما ميل معدوم ![]() على الواجهة، ولكن P(z) تمثل المركبة الناظمية لهذه الأفعال. إن هذه الإجهادات الناظمية تتناسب مع الإجهادات الناظمية الشاقولية خلف الصفيحة والتي يفترض أنها تساوي وزن التربة:
على الواجهة، ولكن P(z) تمثل المركبة الناظمية لهذه الأفعال. إن هذه الإجهادات الناظمية تتناسب مع الإجهادات الناظمية الشاقولية خلف الصفيحة والتي يفترض أنها تساوي وزن التربة:
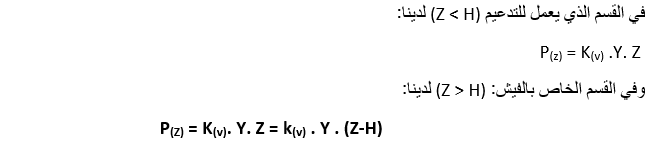
إن قيمة المعامل K(s)والذي يرتبط بالتشوهات المجهولة للصفيحة Y(z) تكون محصورة بين معامل الدفع ks ومعامل الدفع العكسي kp.
وباعتبار : E: عامل المرونة للصفيحة.
I: عزم العطالة للصفيحة.
فإن توازن الجائز يترجم من خلال المعادلة التفاضلية التالية:
![]()
والتي يعطى حلها التشوه Y(z) ومن ثم إجهادات الانعطاف في الصفيحة. ولكي يكون هذا الحل ممكنا، يجب معرفة التابع K(y) والشروط الطرقية للمسألة.
ولكن K(y) تابع غير معروف بشكل جيد، كذلك فالفيش f الذي هو شرط إضافي مجهول أيضا في المسألى، والعطالة I للصفيحة التي تحدد نوع الصفيحة الواجب استخدامها هي أيضا مجهولة.