المستقيمات والمستويات المتقاطعة

​

يتعين الفصل المشترك للمستويين المتقاطعين بإحدى الطرق التالية:

• إن النقاط التي تنتج عن تقاطع آثار المستويين من نفس الاسم هي نقاط من الفصل المشترك للمستويين. (الشكل رقم (1)).
• نقطع المستويين المفروضين بمستو مساعد أفقي أو جبهي ونعين نقطة تقاطع المستقيمين الناتجين فنحصل على نقطة من الفصل المشترك وبنفس الطريقة نحصل على نقطة ثانية.
• نأخذ في أحد المستويين المفروضين مستقيما ما ونعين نقكة تقاطعه مع المستوي الآخر فنحصل على نقطة من الفصل المشترك، وبالطريقة ذاتها نحصل على نقطة ثانية.

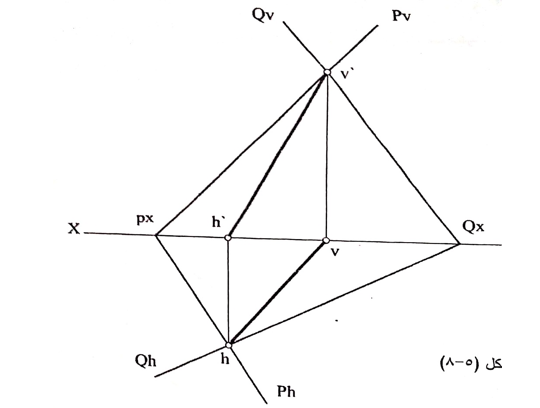
الشكل رقم (1).

ومن الحالات الخاصة لإيجاد الفصل المشترك لمستويين معينين بآثارهما ما يلي:

• الفصل المشترك لمستويين أحدهما شاقولي والآخر أمامي مسقطه الأفقي 12 ينطبق على P_h لأنه يقع في هذا المستوي، ومسقطه الجبهي `2`1 ينطبق على Q_v لأنه يقع في هذا المستوي (الشكل رقم (2)).
• الفصل المشترك لمستويين شاقوليين هو مستقيم شاقولي كما هو مبين في الشكل رقم (3).
• الفصل المشترك لمستويين أماميين هو مستقيم أمامي كما هو مبين بالشكل رقم (4).
• الفصل المشترك لمستويين أحدهما أفقي والآخر كيفي هو عبارة عن مستقيم أفقي، وفي حال كون المستوي P أمامي يصبح الفصل المشترك مستقيما أماميا.
• الفصل المشترك لمستويين أحدهما جبهي والآخر كيفي هو عبارة عن مستقيم جبهي، وفي حال كون المستوي شاقولي يصبح الفصل المشترك مستقيما شاقوليا.
• الفصل المشترك لمستويين أحدهما أفقي والآخر جبهي هو مستقيم موازي لخط الأرض ينطبق مسقطه الأفقي على P_h وينطبق مسقطه الجبهي على Q_v.
• إذا احتوى مستويان على مستقيمين متوازيين فالفصل المشترك لهما يوازي المستقيمين.

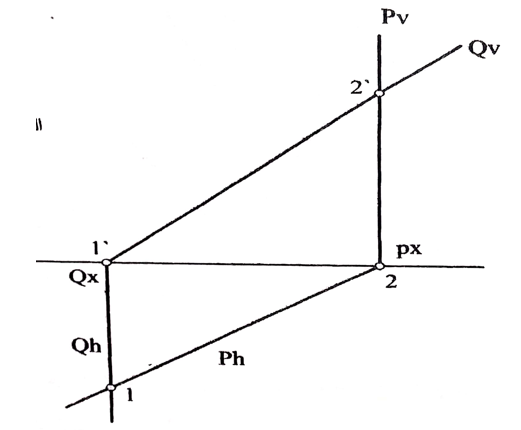
الشكل رقم (2).

​