تصنيف الجوائز حسب المساند
& في حال استناد جائز على مساند بسيطة (مساند بسيطة متحركة) يجب أن لا توازي هذه المساند بعضها البعض وكذلك يجب ألا تتقاطع في نقطة واحدة. ففي حال كون المساند متوازية عندئذ يستطيع الجائز الانتقال وفق خط عمودي على اتجاه قضبان تلك المساند.
وعندما تتلاقى المساند في نقطة واحدة فإن الجائز يستطيع أن يدور بزاوية صغييرة حول النقطة (o)، وهذا غير مسموح به أيضا لأنه في كلتا الحالتين يصبح الجائز غير مستقر هندسيا ويتحول إلى ميكانيزم، الشكل رقم (7).
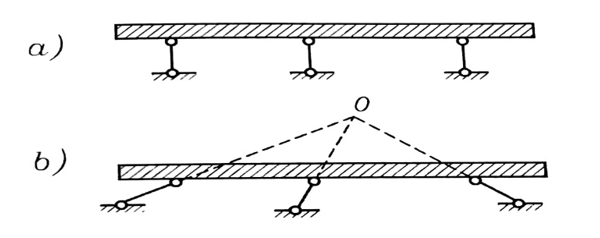
الشكل رقم (7)
إن مسألةحساب ردودأفعال مساند الجوائز المقررة ستاتيكيا تحت تأثير حمولة خارجية معطاة وواقعة في مستو واحد قد حلت بتطبيق معادلات التوازن الستاتيكي وهي:
- مجموع كل من مساقط القوى (حمولات خارجية وردود أفعال المساند) على كل من المحورين (ox) و (oy) يساوي الصفر ومجموع العزوم بالنسبة لأيةنقطة (o) واقعة في مستوي تأثير القوى يساوي الصفر.
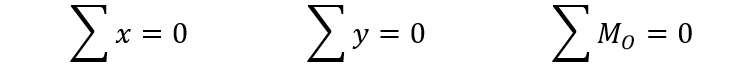
- مجموع عزوم القوى (حمولات خارجية وردود أفعال المساند) بالنسبة لأية نقطتين (A ,B) يساوي الصفر ومجموع مساقط القوى على المحور (X) يساوي الصفر أيضا بشرط ألا يكون المحور (X) عموديا على المستقيم (AB).
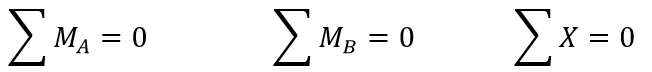
- مجموع عزوم القوى (حمولات خارجية وردود أفعال المساند) بالنسبة لأية ثلاث نقاط (A,B,C) يساوي الصفر، بشرط ألا تقع هذه النقاط الثلاث على مستقيم واحد.
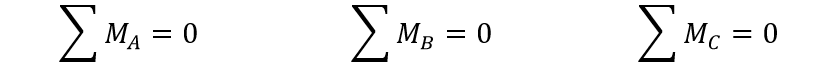
في حالة تعيين ردود أفعال المساند يجب أن نعمل على كتابة معادلات التوازن بحيث يدخل في كل معادلة أقل عدد من ردود الأفعال المجهولة، وللتحقق من صحة ردود الأفعال المحسوبة نقوم بإسقاط جميع القوى على المحور (OY) ويجب أن يساوي مجموع مساقطها الصفر، أي:
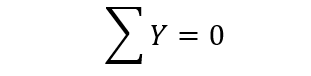
في حال حساب الجائز المركب والمؤلف من عدة جوئز أو قضبان يجب أن نأخذ بعين الاعتبار انه يمكن كتابة معادلات التوازن للجملة ككل ولكل قضيب من قضبان الجملة بشكل منفصل.
في مثل هذه المسائل تكون ردود الأفعال أكثر من ثلاثة وبنفس الوقت فإن المعادلات الستاتيكية المستقلة
قم بتنزيل تطبيق eMufeed Android الآن