حساب الإجهادات المماسية في حالة الانعطاف

  حساب الإجهادات المماسية في حالة الانعطاف

في حالة الانعطاف العرضي تظهر في المقاطع العرضية للجائز قوى قاصة إلى جانب عزم الانعطاف ، وبالتالي بالإضافة إلى الإجهادات الناظمية تظهر إجهادات مماسية في المقاطع الطولية وذلك حسب قانون ازدواج الإجهادات المماسية وتسبب انزياحا للألياف فيما بينها ، نتيجة لذلك لا تبقى المقاطع العرضية مستوية بعد الانعطاف وإنما تعوج وتتحدب ، الشكل رقم (1) ، أي أن فرضية برنولي غير صالحة في هذه الحالة .

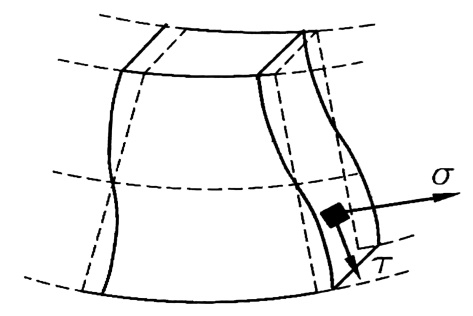
الشكل رقم (1)

ولكن الدراسات النظرية والبحوث التجريبية أثبتت أن تأثير الانزياحات الناتجة عن ظهور الإجهادات المماسية على توزع الإجهادات الناظمية ضئيل جدا لدرجة يمكن إهماله ، وبالتالي فرضية المقاطع المستوية تبقى سارية المفعول ، وتعين الإجهادات الناظمية في حالة الانعطاف العرضي بالعلاقة :

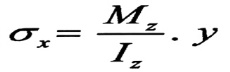
ولتعيين قانون توزع الإجهادات المماسية نقتطع من الجائز المبين بالشكل عنصرا طوله dx ، الشكل رقم

(2-a) ، ونقسمه بشكل طولي إلى جزأين ، ولنبحث توازن أحد الجزأين المقطوعين ولنأخذ مثلا الجزء العلوي الذي تؤثر على جانبيه إجهادات ناظمية ضاغطة .

بما أن عزم الانعطاف على الجهة اليمنى للمقطع أكبر منه على الجهة اليسرى بقيمة مقدارها dM_z . لذلك فإن الإجهادات الناظمية المؤثرة على أية مساحة dA عنصرية واقعة في الجهة اليمنى ستكون أكبر منها على الجهة اليسرى بالمقدار dσ₁ :

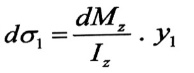
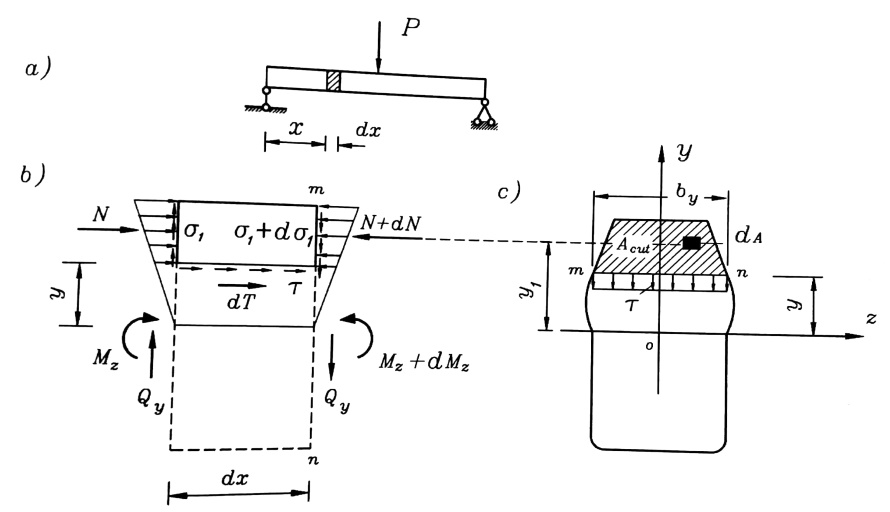
الشكل رقم (2)

وبالتالي القوى الضاغطة المؤثرة على الجزء المقطوع من الجهة اليمنى أكبر منها على اليسرى بمقدار :

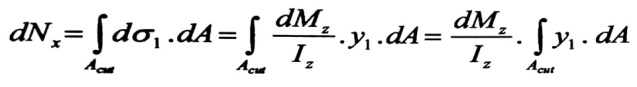
حيث :

A_cut : مساحة الجزء المقطوع من المقطع العرضي (المهشر على الشكل ) .

والتكامل في هذه العلاقة يعبر عن العزم الستاتيكي للجزء المقطوع A_cut بالنسبة للمحور المحايد (oz) .

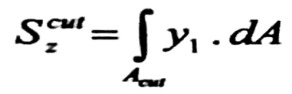
وبالتالي :

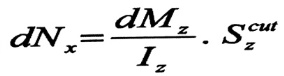
وحتى يكون العنصر المقطوع dx  بحالة توازن يجب أن تؤثر عليه في المقطع الطولي إجهادات مماسية (ꚍ_yx) الشكل رقم (2-b) هذه الإجهادات ستشكل قوة مماسية dT والتي من شرط التوازن x =0∑ يجب أن تكون dT مساوية للقوة dN ، أي :

وبالتالي :

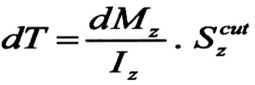
ولتحديد قيمة الإجهادات (ꚍ_yx) لا بد من معرفة قانون توزعها على عرض الجائز ، وبشكل عملي فإن توزع الإجهادات (ꚍ_yx) مرتبط بشكل المقطع العرضي ولكن لمعظم المقاطع العرضية نفترض بأن الإجهادات المماسية موزعة بشكل منتظم على عرض المقطع ، وبهذه الفرضية يمكن حساب قيمة القوى القاصة dT من العلاقة :

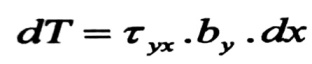
حيث :

b_y : عرض المقطع العرضي في النقطة التي يجري تحديد  الإجهادات المماسية فيها .

ومن العلاقتين السابقتين نجد :