& يتضمن حساب الأساسات المرنة إيجاد المعادلة التفاضلية لإنحناء الأساس، ثم حلها بما يتناسب مع الشروط الطرقية للمسألة المدروسة فنحصل على معادلة تشوه الأساس y(x) وهذا يمكننا من إيجاد القوى الداخلية بجسم الأساس في كل نقطة منه ونفترض بدراستنا أن تشوه الأساس في كل نقطة منه يتساوى مع هبوط التربة.&
& وفي الحالة العامة للمعادلة التفاضلية لانحناء أساس مستمر نفترض أنه لدينا أساس مستمر متغير الصلادة E I(x) وعرضه b خاضع جزء منه لحمولة موزعة وخاضع لحمولات مركزة ولقوة أفقية تؤثر بشكل عمودي على سطح مقطعه العرضي كما في الشكل رقم (1).
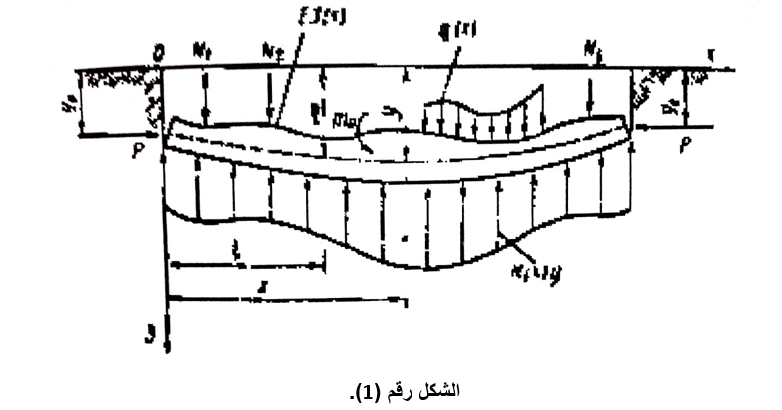
إن التأثير المتبادل بين التربة والأساس يتوافق مع نموذج فوس- ويتكلر (طريقة التشوهات المرنة الموضعية) وإن عامل صلابة التربة K(x) يكون متغيرا مع طول الأساس وإن نسبة ارتفاع الأساس إلى طوله صغيرة أي أن الأساس مرن والمسألة مستوية.
إن الحمولات الخارجية الشاقولية تولد عزم انعطاف قدره M حول أي مقطع من الأساس فوفق الشكل السابق سيؤثر في أي مقطع من الأساس إحداثياته (x,y) عن مبدأ الإحداثيات عزما M(x) مقداره:
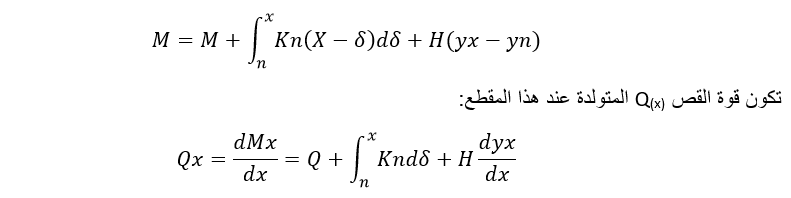
أما الحمولة الموزعة الخارجية المؤثرة على الأساس وبالاعتماد على العلاقة السابقة فتساوي:
قم بتنزيل تطبيق eMufeed Android الآن
