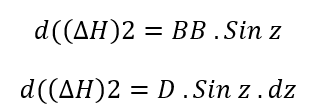ومعنى ذلك أن خطأ متحول لا يؤثر على متحول ثاني وخطأ الخطأ مهمل وخاصة إذا كانت الأخطاء صغيرة جداً.
ليكن لدينا Y تابعا للمتحولات (x1, x2, x3.....xn) أي أن:
Y= f(x1, x2, x3....xn)
لنفترض أنه قمنا بقياس عناصر التابع (x1, x2, x3, ....xn وتحمل هذه القياسات أخطاء صغيرة ولتكن (dx1, dx2, dx3,......dxn) وليكن dy الخطأ الناتج في التابع y باعتبار هذه القياسات لعناصر التابع الحاملة للأخطاء. إذا بإمكاننا أن نكتب وفق للمعادلة السابقة مايلي:
(y+dy)= f(x1+dx1, x2+dx2, x3+dx3....xn+dxn)
ومنه نجد قيمة التغير في التابع dy
Dy= f(x1+dx1, x2+dx2, x3+dx3....xn+dxn)- f(x1, x2, x3, ...xn)
لو قمنا بتطبيق طريقة تايلور بالنشر لهذه القيمة قرب القيم (x1, x2, xn) وبإهمال اللامتناهيات في الصغر من الدرجة الثانية نجد أن :
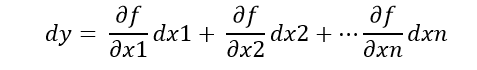
نلاحظ من العلاقة السابقة أن الخطأ المرتكب على التابع y لعدة قياسات (x1, x2, x3,....xn) هو التفاضل الكلي للتابع بالنسبة للقياسات. ويمكننا اعتبار هذه النتائج صحيحة إذا كانت الأخطاء ذات قيم صغيرة كما ذكرنا سابقا، ونلاحظ أن قيمة الخطأ في التابع dy هي تابع خطي لأخطاء القياسات dx1, dx2, dxn وكل خطأ يؤثر بشكل مستقل على النتيجة..
إن الفرضية الموجودة في العلاقة السابقة لا تكون حقيقية إلا إذا كانت الأخطاء صغيرة جدا ونسميها بفرضية استقلال الأخطاء ونلاحظ أيضاً أن هذه الفرضية أنه لم يتم التمييز بي الأخطاء النظامية و الأخطاء العرضية مما يدعنا نقول أن كيفية تأثير الخطأ على النتائج هو مستقل عن طبيعة الخطأ فخطأ قيمة معروفة لا يمكن أن يؤثر إلا بطريقة واحدة على النتيجة.
ومثالاً على فرضية استقلال الأخطاء ، لنفترض أننا نريد تعيين فرق الارتفاع دلتا H بين النقطتين A, B كما هو مبين بالشكل المبين فيما يأتي، ولذلك قسنا الزاوية z والمسافة D بين النقطتين A, B ، من الشكل نجد أن:
![]()
فإذا فرضنا أن dz, d(D) هي أخطاء مرتكبة على المسافة والزاوية بالترتيب وبتطبيق العلاقةdy نجد:
![]()
نلاحظ من العلاقة السابقة أن كل خطأ يكون مستقل عن الآخر وأن الخطأ الناتج عن فرق الارتفاع دلتا H بسبب خطأ في المسافة (Cosz.d(D)) وهذا ما يوضحه الشكل التالي باعتبار أن dz=0 اي أننا نحصل على القيمة ![]() وكذلك بالنسبة لتأثير الخطأللزاوية نجد باعتبار أن d(D) يساوي الصفر أن الخطأ الناتج في فرق الارتفاع الناتج عن خطأ في الزاوية هو D.Sin z.d z وهو ما يوضحه الشكل التالي حيث أن :
وكذلك بالنسبة لتأثير الخطأللزاوية نجد باعتبار أن d(D) يساوي الصفر أن الخطأ الناتج في فرق الارتفاع الناتج عن خطأ في الزاوية هو D.Sin z.d z وهو ما يوضحه الشكل التالي حيث أن :