بالإضافة إلى كون منحنيات التسوية تمثل لنا تضاريس سطح الأرض في المنطقة المدروسة كذلك تعطي فكرة عامة عند التخطيط الأولي لمعظم المشاريع الهندسية ومن هذه الفوائد ما يلي:
- تعيين ارتفاع النقاط: عند تعيين ارتفاع النقاط بواسطة منحنيات التسوية من الممكن أن نصادف الحالات التالية:
- النقطة واقعة على منحني التسوية مباشرة فعندها يكون ارتفاع النقطة هو ارتفاع التسوية.
- النقطة B تقع بين منحني ذو الارتفاعين h1=256, h2=258 كما هو مبين بالشكل رقم (1) فعندئذ بحسب ارتفاع النقطة بالتوسط الداخلي. في هذه الحالة لتعيين ارتفاع النقطة B علينا أن نقيس المسافات الأفقية d1 و d من النقطة B وحتى أقرب منحنب تسوية وذلك بواسطة المسطرة بحيث تكون المسافة عمودية نوعا ما على منحني التسوية. وعندها يحسب ارتفاع النقطة B من العلاقة التالية: H1= h1 + d1/d .e
أي أن HB= 256 + d1/d.e
حيث أن: d1 : هي المسافة الأفقية من منحني التسوية 256 وحتى النقطة B, d: المسافة الأفقية بين منحني التسوية 256 و258.e : هي التباعد الثابت ما بين منحني التسوية وفي المثال تساوي 2 متر.
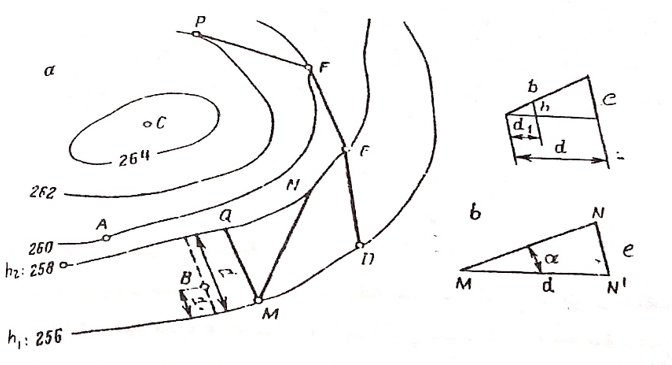
الشكل رقم (1)
- النقطة c واقعة داخل منحني التسوية المغلق فإذا كانت النقطة c أعلى من منحني التسوية المغلق فيمكن اعتبار ارتفاعها بشكل تقريبي يساوي إلى ارتفاع منحني التسوية مضافا إليه نصف التباعد الثابت وفي المثال مثلا يكون ارتفاع النقطة c مساويا إلى: Hc = 264 +e/2=256
وذلك باعتبار أن e تساوي إلى 2 متر. وإذا كانت النقطة c أخفض من منحني التسوية الواقعة ضمنه فيكون ارتفاعها بشكل تقريبي يساوي إلى ارتفاع منحني التسوية مطروحا منه نصف التباعد الثابت. وإن دقة تعيين ارتفاع نقطة من منحنيات التسوية تساوي إلى e/3 حيث e التباعد المتساوي ما بين منحنيات التسوية.
- قياس الميول على المخطط: يمكن قياس ميل سطح الأرض الطبيعية فمثلا لقياس ميل الخط MN على المخطط في الشكل السابق فيكون الميل (i) عن الأفق وفق زاوية معينة مساويا إلى : i=e/d وهو ظل الزاوية. فمثلا إذا كانت MN=d=223 m عندها يكون ميل الأرض وفق الخط MN يساوي إلى: i= (258- 256)/223=2/223=0.009 أو يكتب i=9%o حيث تكتب الميول بشكل عام على شكل رقم منسوبا من ألف.
- رسم خط وفق ميل معطى على المخطط: عند تخطيط المنشآت ذات الطابع الخطي على المخططات الطبوغرافية نضطر أحيانا إلى رسم مسارات معينة وفق ميول محددة فمثلا من النقطة D باتجاه النقطة P (في الشكل السابق) علينا أن نرسم المسار المؤلف من عدة مستقيمات وفق ميل i=12%o لتحقيق ذلك نعمل ما يلي:
نقيس المسافة الأفقية d بواسطة الفرجار وفق مقياس الرسم المحسوبة من العلاقة التالية: d=e/i حيث i الميل المعطى و e قيمة التباعد الثابت. ففي المثال السابق e=2m و i=12%o نجد أن d=166.66 m.
وفق مقياس المخطط نأخذ المسافة ونعبر عنها بفتحة الفرجار ونبدأ بالنقطة D وتقاطع منحني التسوية المجاور وذلك بواسطة الفرجار وفق المسافة 166.66 متر فنحصل على النقطة E وبالطريقة نفسها نحصل على النقاط F و P وبهذا نكون قد حصلنا على المسار DEFP وفق الميل المعطى.
من فوائد منحنيات التسوية أيضا ما يلي:
رسم المقاطع بواسطة منحنيات التسوية وفق خط معطى: من أجل رسم المقاطع لسطح الأرض وفق خط معطى AB كما في الشكل رقم (2) نحسب جميع المسافات الأفقية التي يشكلها خط المقطع AB ونرسم خطا أفقيا على ورقة بنفس الطول المقاس على المخطط ومن ثم نختار مقياسا شاقوليا مناسبا لبيان ارتفاع نقاط تقاطع الخط AB مع منحنيات التسوية.ونعتبر أن الخط الأفقي للطول AB ممثلا لمستوي المقارنة بحيث يكون ارتفاعه أخفض من ارتفاع أي نقطة من نقط التقاطع بخمسة سنتيمتر تقريبا على ورقة الرسم وبعد ذلك نقوم بما يلي:









