للحصول على علاقة أساسية لكمية التسرب عبر كتلة من التربة في حالة معينة ندرس الحالة المبينة في الشكل 1 حيث مساحة المقطع العرضي للتربة مساوية لـ (A) ومعدل التسرب هو q، وكما رأينا فإن الضغط الكلي للجريان في أي مقطع من التربة يعطى بعلاقة برنولي على النحو التالي:
الضاغط الكلي= الضاغط المكاني + الضاغط المائي + الضاغط الحركي
وبإهمال الضاغط الحركي ( الناتج عن سرعة الجريان خلال التربة) يكون الضاغطان الكليان في المقطعين (A, B) على النحو التالي:
الضاغط الكلي عند المقطع A: Za+Ua
الضاغط الكلي عند المقطع B: Zb+Ub
حيث(Zb, Za) هما الارتفاعان الجغرافيان للنقطتين عن مستوى مقارنة ما.
:(Ua, Ab) هما الضاغطان المائي أو البيزومتري عند النقطتين (A, B). حيث إن فرق الضاغط الهيدروليكي 
بين المقطعين (A,B) هو:
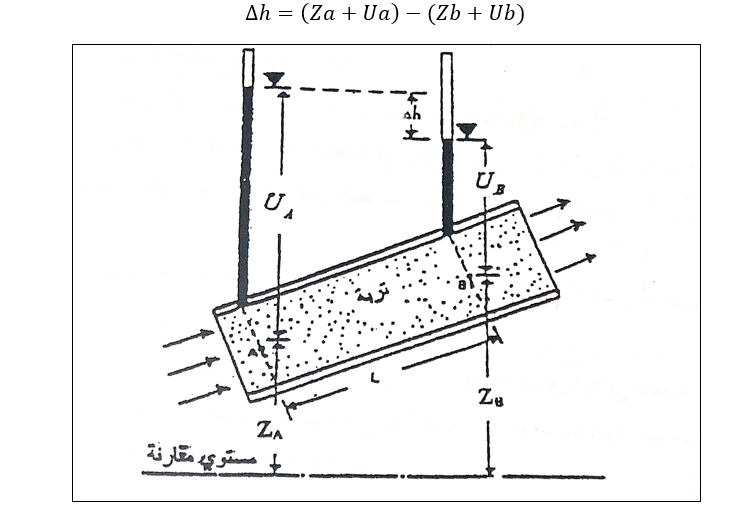
الشكل 1: شرح قانون دارسي
ويمكن أن تكتب الميل الهيدروليكي كالتالي: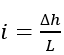 
حيث أن (L) المسافة بين المقطعين (A,B).
لقد أوجد دارسي علاقة بسيطة بين التسرب والميل الهيدروليكي من أجل الجريان وحيد الاتجاه حيث قال بوجود تناسب بين سرعة انخفاض الضغط والميل الهدروليكي على النحو التالي: 
حيث 
سرعة التسرب أو سرعة انخفاض الضاغط.
I الميل الهيدروليكي
K عامل النفوذية
وبذلك يكون معدل التسربq كالتالي:
مع الملاحظة أن A هي المقطع العرضي للتربة العمودي على اتجاه الجريان . إن عامل النفوذية k له وحدات السرعة التالية:cm/sec,mm/sec وهو مقياس لمقاومة التربة لجريان الماء فيها .
وعندما تعطى خواص المياه المؤثرة في الجريان نستطيع أن نعبر عن معامل النفوذية (k) بالعلاقة التالية:
قم بتنزيل تطبيق eMufeed Android الآن
