الانعطاف المائل
يعرف الانعطاف المائل بأنه تلك الحالة من انعطاف الجائز التي عندها يكون مستوي تأثير محصلة عزم الانعطاف في المقطع لا ينطبق مع أحد محاوره الرئيسية .
وفي هذه الحالة يمكن تحليل محصلة عزم الانعطاف إلى عزمي انعطاف MZ , My ، يؤثران في المستويين الرئيسين المارين بالمحاور الرئيسية للمقطع ، فمثلا المدادات الموضحة بالشكل رقم (1) تعمل على الانعطاف المائل ، إذ أن الحمولة الشاقولية الناتجة عن وزن التغطية والوزن الذاتي للمداد تميل على المحاور الرئيسية بزاوية α ، كذلك فالجائز الظفري ذو المقطع الزاوي ، الشكل رقم (2) ، سيتعرض لانعطاف مائل تحت تأثير وزنه الذاتي حيث أن المحاور الرئيسية للمقطع الزاوي تميل بالنسبة للحمولة بزاوية مقدارها α .
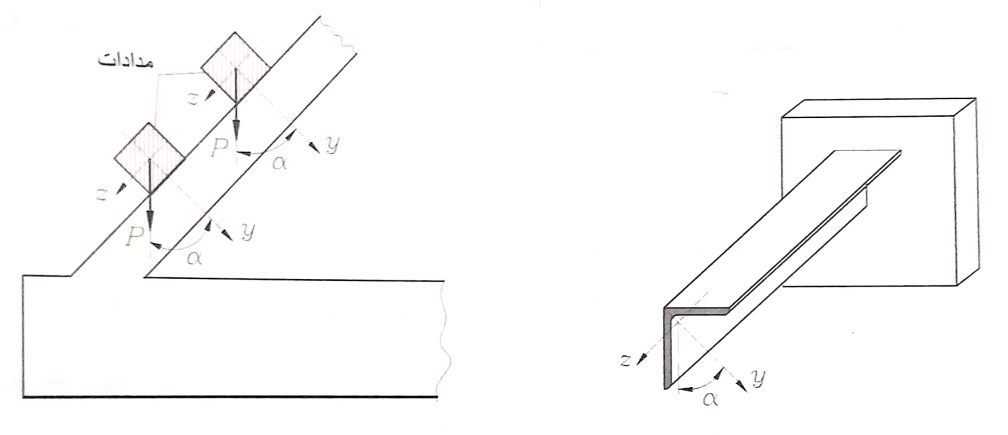
الشكل رقم (2) الشكل رقم (1)
تعيين الإجهادات في حالة الانعطاف المائل :
نبحث في جائز ظفري مثبت من طرف وعلى الطرف الآخر تؤثر قوة P مطبقة في مركز ثقل المقطع ، وتميل عن المحور y بزاوية α ، الشكل رقم (3) .
نحلل القوة P إلى مركبتين :
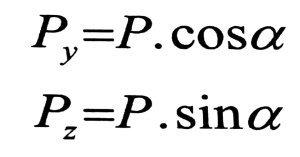 (1)
(1)
وبالتالي فعزمي الانعطاف في المقطع I – I بالنسبة لكل من محوري العطالة الرئيسين هما :
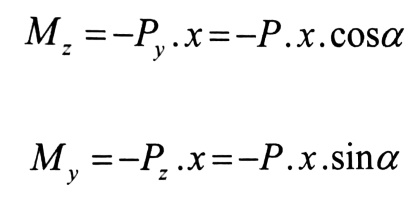 (2)
(2)
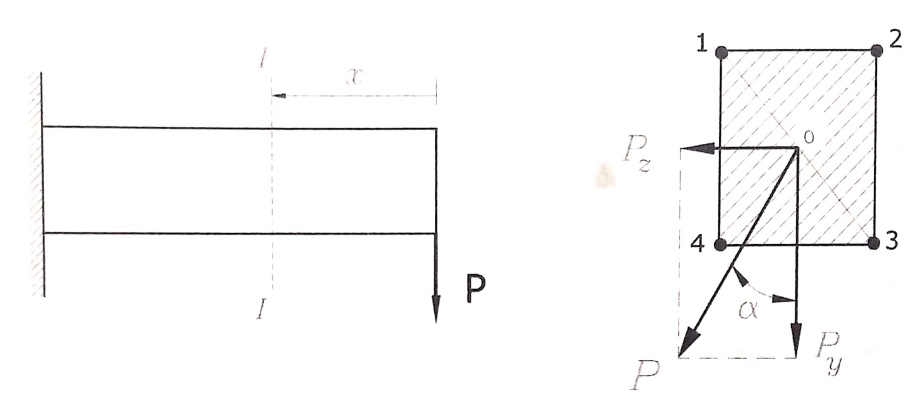
الشكل رقم (3)
وهكذا ، في وقت واحد ، يؤثر في كل مقطع عرضي عزمي انعطاف يؤديان إلى انحناء الجائز في المستويين الرئيسين .
من أجل تحديد الإجهادات من كل عزم على حدة يمكن استعمال العلاقة المستخرجة في حالة الانعطاف المستوي ، وباستعمال مبدأ جمع الآثار يمكن كتابة الصيغة العامة للإجهادات في أي نقطة تقع في الربع الموجب من جملة المحاور الإحداثية :
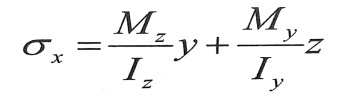 (3)
(3)
وحسب هذه العلاقة يمكن تحديد الإجهادات في أي نقطة من نقاط المقطع وذلك بتعويض قيمة إحداثياتها الجبرية ، وبما أن القيمة المطلقة (z,y) لإحداثيات النقاط الركنية أعظم ما يمكن ، فإنه يمكن كتابة العلاقة رقم (3) بالشكل التالي :









