التحقق من متانة الجوائز عند الانعطاف
المقطع العرضي للجائز متناظر بالنسبة للمحور المحايد :
إن تناظر أو عدم تناظر المقطع العرضي للجائز بالنسبة لمحور محايد يتعلق بشكل أساسي بخواص المادة المصنوع منها ، فإذا كانت خواص المادة على الشد وعلى الضغط متساوية ، فمن الأفضل أن يكون متناظراً ، وبالعكس .
وعندما كانت العلاقة التي نعين بها قيمة الإجهادات الناظمية هي :
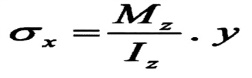
وبالتالي في مقطع معين تكون أكبر قيمة للإجهادات الناظمية ، بالقيمة المطلقة ، هي الموافقة لأبعد نقطة ymax عن محور المحايد ، أي :
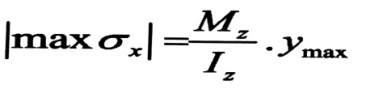
أو :
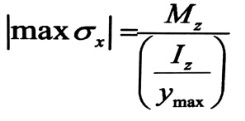
ولكن :
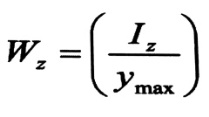
حيث :
Wz : العزم المقاوم للمقطع .
لتأمين متانة الجائز عند الانعطاف من الضروري أن لا تزيد الإجهادات الشادة العظمى والإجهادات الضاغطة العظمى ، في المقطع الخطر ، عن الإجهادات المناظرة والمسموح بها ، أي :
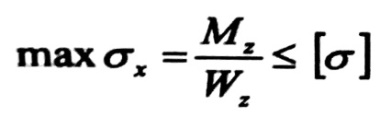
حيث :
[σ] = [σc] = [σt] : الإجهادات المسموح بها على الضغط أو الشد ، وهي تتعلق بشكل أساسي بمادة الجائز وأهميته .
ملاحظة :
آخر مقطع هو المقطع الذي تكون فيه قيمة Mz عظمى ، ولك في حال كون المقطع العرضي للجائز ثابت على كامل طوله .
ولدى دراسة العناصر التي تعمل على الانعطاف تصادفنا المسائل التالية :
التحقق من متانة الجائز :
حيث تعطي أبعاد المقطع العرضي والحمولات المطبقة ونرسم مخطط عزوم الانعطاف التي تظهر في مقاطعه العرضية وذلك لنعين أكبر عزم |max Mz|، عندئذ تحسب قيمة الإجهادات الأعظمية من العلاقة :
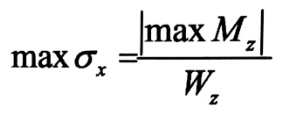
ثم نقارن قيمة الإجهاد الحاصل مع الإجهاد المسموح به لمادة الجائز ، ويكون محققا على المتانة إذا حقق العلاقة التالية :
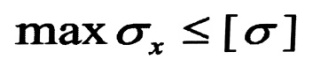
اختيار أبعاد المقطع العرضي :
لاختيار أبعاد المقطع نعين عزمه المقاوم المطلوب Wz ، من العلاقة :
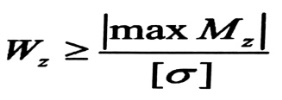
وبتعيين عزمه المقاوم نستطيع تعيين أبعاده أو اختياره مباشرة من الجداول الجاهزة .
تعيين الحمولة المسموحة :
عند تعيين أكبر حمولة – الحمولة المسموحة – يمكن أن يتحملها جائز ما ، نأخذ أكبر قيمة مطلقة لعزم الانعطاف من مخطط العزم ، ونكتبها بشكل تابع للحمول المؤثرة (حمولة موزعة بانتظام ، أو مركزة ، أو عزم مركز ) ونساوييها بقيمة عزم الانعطاف المسموح به ، والمعطى بالعلاقة :
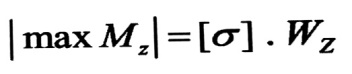
- في بعض الحالات الخاصة وعلى سبيل المثال ، حالة مقطع I ، الشكل رقم (1) ، من الضروري إجراء التحقيق على المتانة في مجموعة من النقاط المميزة في المقطع العرضي ، حيث تلعب الإجهادات المماسية دورا هاما .
- ففي النقطة 1 ، الإجهادات المماسية تساوي الصفر والحالة الإجهادية في هذه النقطة هي حالة محورية ، وبالتالي التحقق على المتانة يجري وفقا للإجهادات الناظمية فقط حسب العلاقة :









