مثال تطبيقي حول الإطارات المستوية
يطلب تعيين ردود الأفعال ورسم مخططات عزوم الانعطاف وقوى القص والقوى الناظمية في الإطار المبين بالشكل رقم (1) وذلك باستخدام طريقة الأظفار .
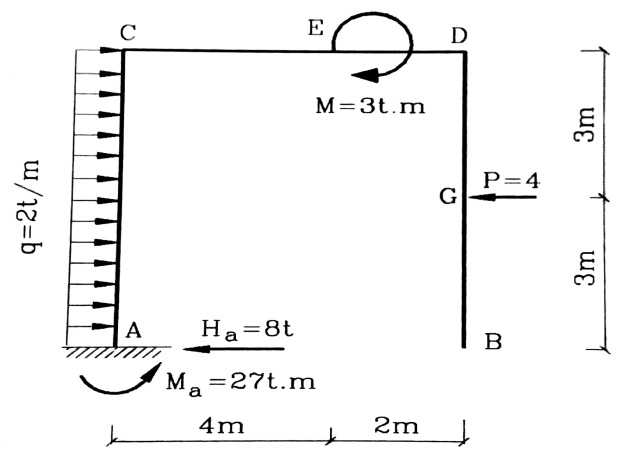
الشكل رقم (1)
الحل :
يمكن دراسة هذا الإطار بتقسيمه إلى ثلاثة جوائز هي AC و CD و DB ، حيث تتم دراسة كل منها على حدة بدءا من الجائز الأيمن في الإطار (وهو DB) وانتهاء بالجائز الأيسر فيه (وهو AC) ، وعندئذ لا حاجة لتعيين ردود الأفعال في المسند A قبل البدء بدراسة القوى الداخلية حيث أن هذه الدراسة تتم بدءا من الطرف الحر .
دراسة الجائز DB :
تتم دراسة هذا الجائز باعتباره جائزا ظفريا موثوقا من الطرف D وحرا من الطرف B وذلك تحت تأثير الحمولة الخارجية P = 4t المطبقة في المقطع G منه ، الشكل رقم (2-a) ، فإذا اعتبرنا محور الإحداثيات واقع عند الطرف الحر B ، يكون :
- في المجال GB ، حيث : 0 ≤ x ≤ 3 m .
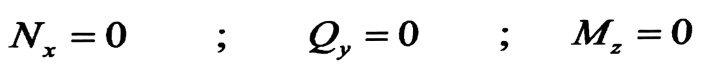
- في المجال DG ، حيث : 3m ≤ x ≤ 6m .
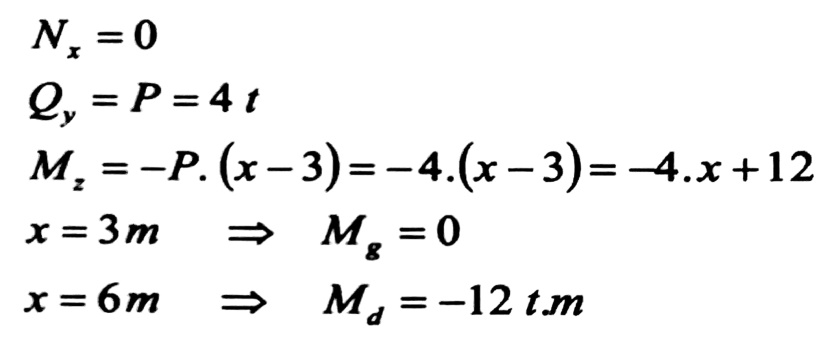
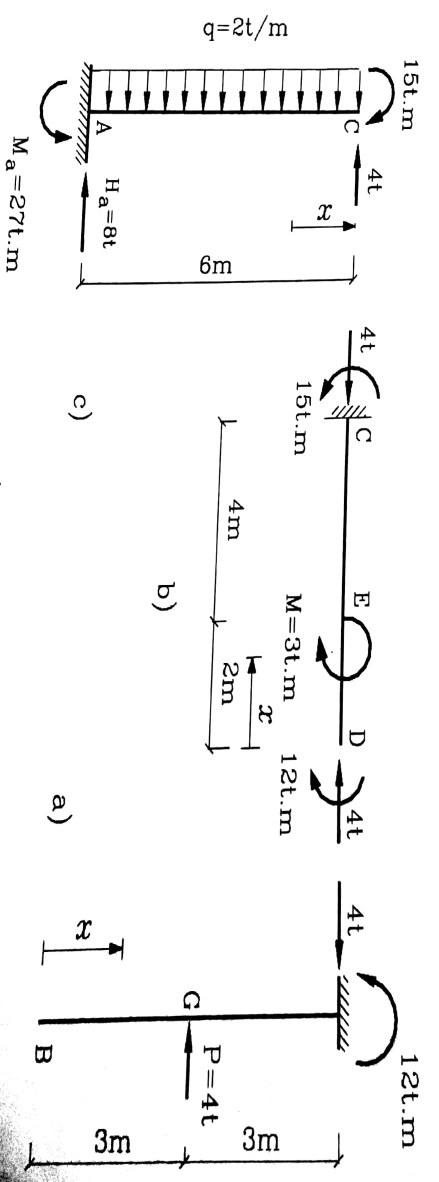
الشكل رقم (2)
دراسة الجائز CD :
تتم دراسة هذا الجائز باعتباره جائزا ظفريا موثوقا من الطرف C ، وحرا من الطرف D وذلك تحت تأثير المزدوجة الخارجية M = 3 t.m المطبقة في المقطع E منه إضافة إلى الحمولات المنقولة إليه من الجائز DB ، كما في الشكل رقم (2-a) .
فإذا افترضنا محور الإحداثيات x مواز لمحور الجائز CD ، ومبدأ الإحداثيات واقع عند الطرف الحر D ، نحصل على :
- في المجال DE ، حيث : 0≤ x ≤ 2 m .
NX = ‒4 t ; Qy = 0 ; Mz = ‒12 t.m
- في المجال CE ، حيث : 2m ≤ x ≤ 6m .
NX = ‒4 t ; Qy = 0 ; Mz = ‒15 t.m
دراسة الجائز AC:
تتم دراسة هذا الجائز الظفري الموثوق من الطرف A وذلك تحت تأثير الحمولات









