المسائل غير المقررة ستاتيكيا
عند دراسة الفتل كثيرا ما نصادف ، كما هي حالة الشد ، مسائل لا يمكن حلها بمساعدة معادلات التوازن وحدها فقط . في مثل هذه المسائل يزيد عدد المجاهيل على عدد معادلات التوازن وتدعى هذه الحالة عندئذ بالمجموعة غير المقررة ستاتيكيا . إن طريقة حل مثل هذه المسائل ، هي نفس الطريقة التي استعملت في حل المسائل غير المقررة ستاتيكيا عند الشد أو الضغط .
مثال (1) :
قضيب فولاذي موثوق من الطرفين ويتعرض لعزم فتل مقداره M = 44 Kgf.m ، الشكل رقم (1) .
المطلوب تعيين ردود الفعل في المسندين A و B ، ورسم مخطط عزوم الفتل الداخلية .
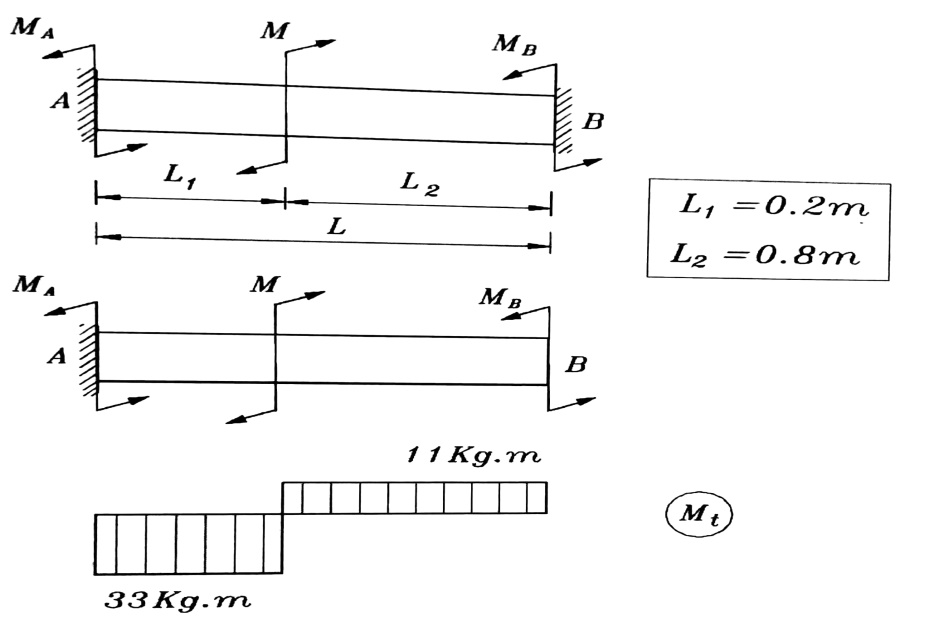
الشكل رقم (1)
الحل :
إن طريقة حل غير المقررة ستاتيكيا تحت تأثير عزوم الفتل تتم بصورة مشابهة للعناصر غير المقررة ستاتيكيا تحت تأثير القوى الشادة أو الضاغطة .
نرمز لردود الفعل عند المسند A و B بعزوم الفتل MA و MB . ومن أجل تعيين هذه العزوم لدينا معادلة توازن واحدة وهي :
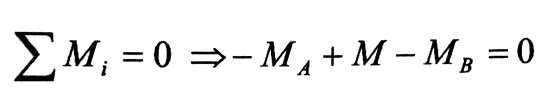
ومنه :
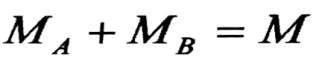 (1)
(1)
المعادلة رقم (1) تحوي مجهولين ولحلها نشكل معادلة أخرى عن طريق تشوهات القضيب . ومن أجل هذا نحذف إحدى الوثاقتين ولتكن B ونعوض عنها بعزم الفتل MB .
وتعين قيمة عزم الفتل هذا من الشرط التالي : إن زاوية دوران المقطع عند الوثاقة B نتيجة تأثير العزوم M و MB تساوي الصفر وذلك لأن هذا المقطع هو في الأصل موثوق وبالتالي ممنوع من الدوران .
تعين زاوية دوران المقطع B للطرف الحر من العمود على أساس مبدأ التأثير المستقل للقوى (مبدأ جمع الآثار) كمجموع حدين :
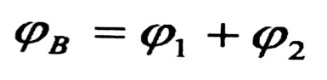
حيث :
ϕ1 و ϕ2 زوايا دوران المقطع نتيجة التأثير المستقل للعزمين M و MB ، ومن هذا نجد :
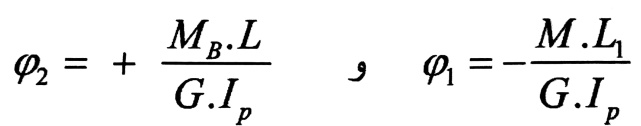
- الإشارة السالبة أخذت في العلاقة لأن العزمين M و MB يؤثران بشكل متعاكس بالاتجاه .
وبالتالي زاوية الفتل الكلية للمقطع عند الطرف الحر للقضيب تساوي الصفر ، أي :
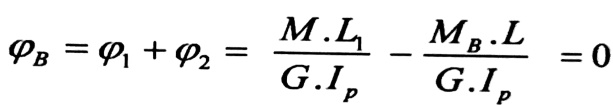
ومنه :
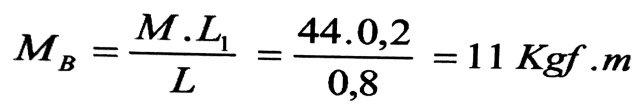
ومن ثم نرسم مخطط عزوم الفتل الداخلية كما هو موضح على الشكل رقم (1).
مثال (2) :
لدينا قضيب معدني قطره D = 2,8 cm وطوله 25 cm ، حملناه على الشد والفتل فحصلنا على النتائج التالية :
-1 من أجل قوة p = 50 kgf كان التطاول الكلي ∆L = 0,04 cm .
-2 من أجل عزم فتل Mt = 12,50 kgf.cm كانت قيمة زاوية الفتل الكلية ϕ = 1,51o .
المطلوب :
-1 حساب قيمة عامل المرونة E.









