تعيين قوة الشد H أو السهم f
من الناحية الهندسية :
لإيجاد العلاقة التي تربط بين طول السلك المعلق S ومسقطه الأفقي L والسهم f في منتصف المجاز ، وذلك بأخذ طول عنصر صغير من المنحني والذي يعبر عنه بالعلاقة التالية :
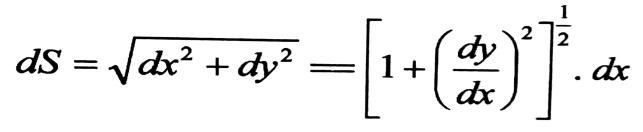
وإذا كان السلك قليل التدلي ، فإن المقدار 2(dy/dx) سيكون صغيرا جدا مقارنة بالواحد . وبنشر العلاقة بشكل كثير حدود نيوتن وأخذ الحدين الأوليين من المنشور نجد :
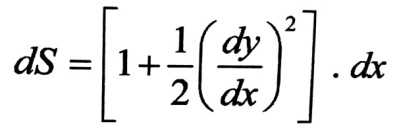
وبإيجاد dy/dx من اشتقاق العلاقة رقم ((8) من المقال (المعادلات الأساسية في حساب الأسلاك اللينة)) ، وبتعويض الناتج في العلاقة السابقة ومكاملتها على كامل طول المجاز ، نجد :
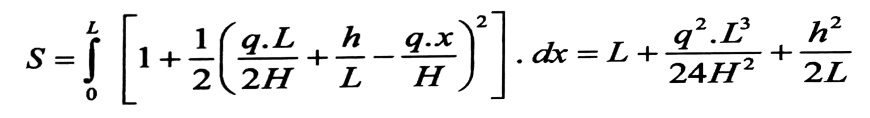
وبتعويض :
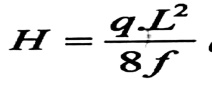
في العلاقة السابقة نحصل على :
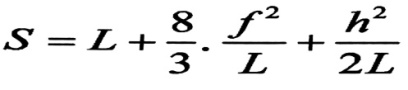 (2)
(2)
وبالتالي من الناحية الهندسية تكون الاستطالة المطلقة ∆S لسلك ، بعد تعليقه ، هي:
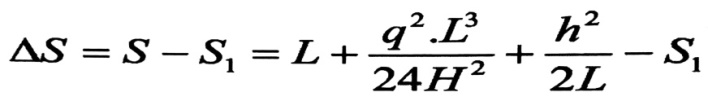 (3)
(3)
حيث :
S1 : الطول البدائي للسلك المعلق أو المثبت .
من الناحية الفيزيائية :
لمعرفة التشوه الكلي في السلك لا بد من دراسة التأثير المشترك للقوة الشادة مع تغير درجة الحرارة .
نعين استطالة السلك معتبرين أن طول السلك يساوي المسافة الكائنة بين نقاط المساند L1 (أو ما يسمى بخط الاستناد) ، وبفرض أن القوة الداخلية فيه ثابتة وتساوي H (هذا الفرض من أجل تبسيط الحل والخطأ الناتج عنه يمكن إهماله) ، الاستطالة المطلقة الناتجة عن تأثير H تعين بالمعادلة التالية :
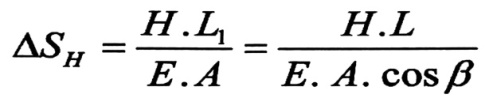 (4)
(4)
أما التشوه الكلي الناتج عن تغير درجة الحرارة ، وكما هو معروف يتعين بالمعادلة :
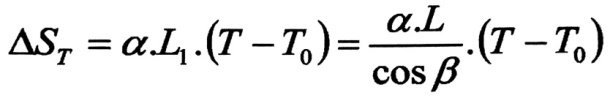 (5)
(5)
حيث :
α : معامل التمدد الحراري لمادة السلك .
To : درجة الحرارة لحظة تعليق السلك .
T : درجة الحرارة التي يجري عندها الحساب .
وبالتالي نحصل على التشوه الكلي للسلك من المجموع الجبري للتأثيرين السابقين :
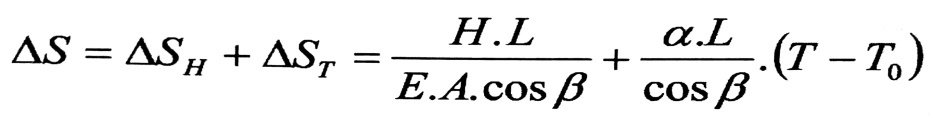 (6)
(6)
ومن تساوي المعادلتين (3) و (6) ، ينتج :
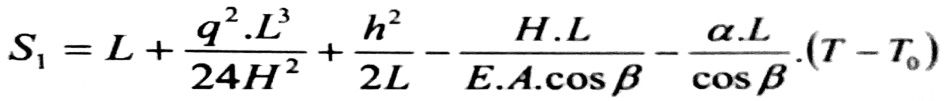 (7)
(7)
النتيجة :
باستخدام المعادلة رقم (3) مع المعادلة (6) يمكن تعيين قوة الشد H أو السهم f .
وبعد معرفة المركبة الأفقية H لقوة الشد يمكن إيجاد قوة الشد الأعظمية max T(z) من المعادلة رقم ((12) من مقال المعادلات الأساسية في حساب الأسلاك اللينة) .
التحقق من متانة السلك :
وللتحقق من شرط متانة مقطع السلك نستخدم العلاقة التالية :
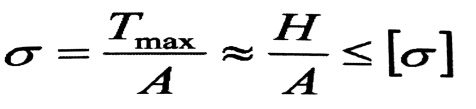
وبتعويض قيمة H من المعادلة رقم ((12) من مقال المعادلات الأساسية في حساب الأسلاك اللينة) يكون شرط المتانة :
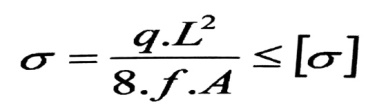 (8)
(8)
وبإدخال مفهوم الوزن النوعي ، حيث ȳ = q/A ، فإن شرط المتانة يأخذ الصيغة التالية :









