مثال تطبيقي حول الطريقة الثالثة لدراسة الجوائز المركبة
مثال :
ليكن الجائز المركب المبين على الشكل رقم (1) ، والمطلوب :
-1 رسم مخطط عزوم الانعطاف وذلك بطريقة جمع الآثار .
-2 رسم مخطط قوى القص انطلاقا من مخطط عزوم الانعطاف .
-3 تعيين ردود الأفعال في المساند اعتمادا على مخطط قوى القص .
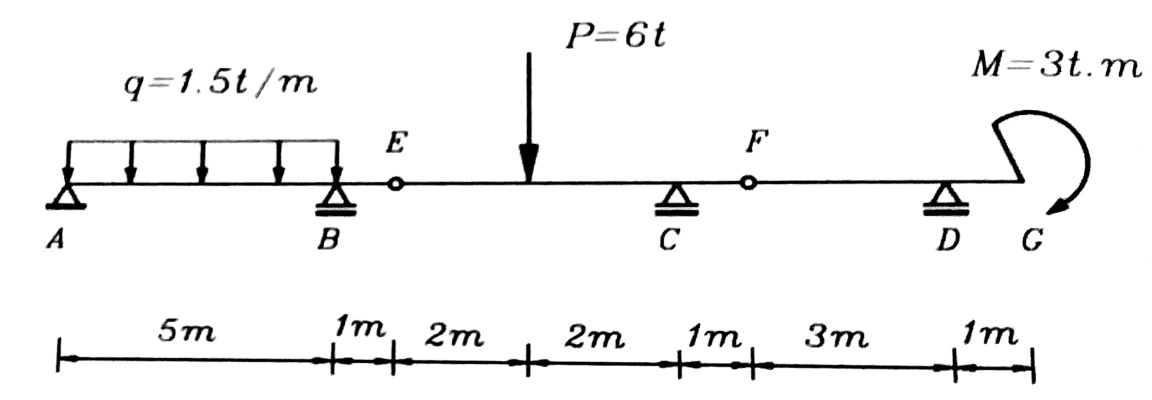
الشكل رقم (1)
الحل :
- رسم مخطط عزم الانعطاف :
إن الجائز المبين يتألف من جائز ثانوي FG يستند على الجائز الثانوي EF في المفصل F ، وجائز ثانوي EF يستند على الجائز الرئيسي AE في المفصل E أي أن الحمولات ستنتقل من الجائز FG إلى الجائز EF ومن ثم إلى الجائز AE ، وبالتالي :
العزم المركز M المطبق على الجائز FG سيؤثر على الجائزين EF ، AE ويكون مخطط عزم الانعطاف تحت تأثير هذا العزم كما هو مبين في الشكل رقم (2-a) ، والقوة المطبقة P على الجائز الثانوي EF ستؤثر على الجائز AE والشكل رقم (2-b) يبين مخطط عزم الانعطاف في الجائز المركب تحت تأثير P ، والحمولة الموزعة q تؤثر فقط على الجائز الرئيسي .
يبين الشكل رقم (2-c) شكل مخطط عزم الانعطاف للجائز المركب تحت تأثيرها ، وبجمع المخططات الثلاثة السابقة جبريا نحصل على مخطط عزم الانعطاف للجائز المركب تحت تأثير الحمولات الخارجية كما في الشكل رقم (2-d) .
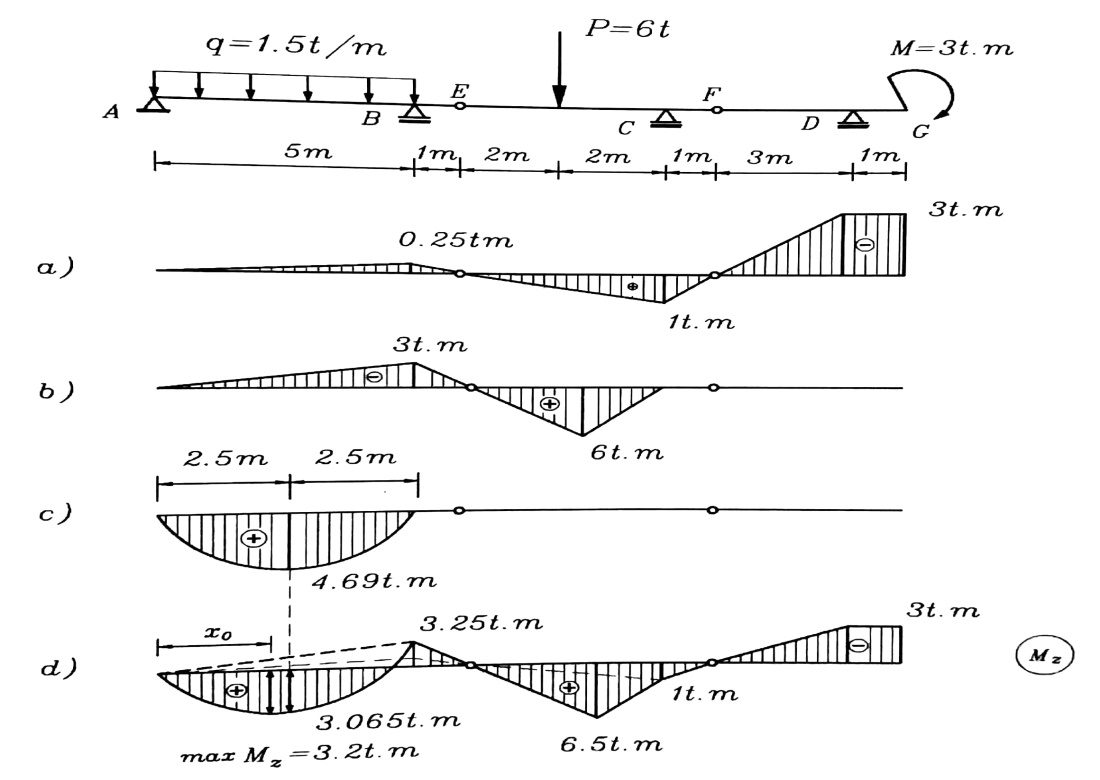
الشكل رقم (2)
- رسم مخطط قوى القص :
من مخطط عزم الانعطاف السابق يمكن أن نرسم مخطط قوى القص وذلك بأن نحدد ميل المماس لمنحني العزم في مجالات الجائز المختلفة لأن :
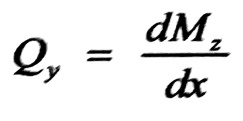
كما يلي :
المجال AB :
إن مخطط عزم الانعطاف هو قطع مكافئ من الدرجة الثانية وبالتالي مخطط القص سيكون بشكل مستقيم ميله يساوي شدة الحمولة الموزعة q ، وهو متناقص باتجاه المحور x (من اليسار إلى اليمين ) وذلك لأن اتجاه القوة الموزعة نحو الأسفل . ولرسم هذا المستقيم يكفي تعيين نقطة لأن ميله معروف وهي نقطة انعدام القص على بعد xo من A حيث يكون العزم أعظميا ويمكن تحديد xo بطريقتين :
-1 تخطيطيا : إذا كان المخطط مرسوما بدقة فإن : xo = 2.067 وبالتالي :
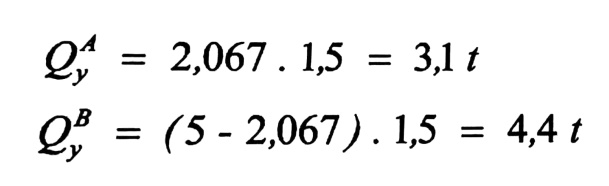
-2 تحليليا : نكتب معادلة القطع المكافئ في المجال AB (بطريقة جمع الآثار) :
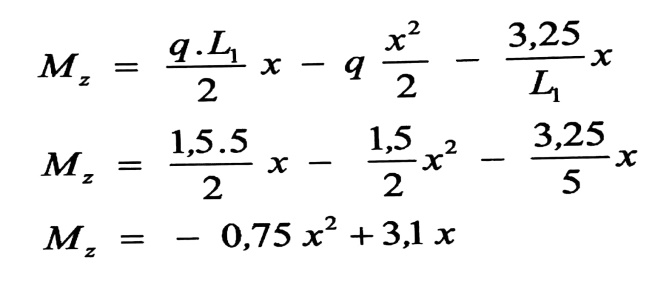
وتكون معادلة قوى القص :









