المعادلة التفاضلية لمحور الجائز المنحني (الخط المرن)
عند استنتاج علاقات الإجهادات الناظمية عند الانعطاف ، حصلنا على العلاقة التي تربط بين التقوس وعزم الانعطاف وهي :
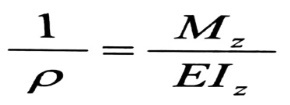(1)
إن العلاقة رقم (1) تظهر بأن التقوس 1/P يتغير على طول الجائز بنفس القانون الذي تتغير فيه قيمة :
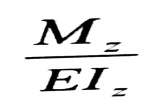
- ففي الجائز ذي المقطع العرضي الثابت والمبين بالشكل رقم (1-a) نلاحظ أن مخطط التقوس 1/P ، الشكل رقم (1-c) ، له نفس شكل مخطط العزم ، الشكل رقم (1-b) ، فإذا كان الجائز ذا مقطع عرضي ثابت ويتعرض لانعطاف صافي ، الشكل رقم (1) ، فإن قيمة العزم على طوله لا تتغير ، وبالتالي تقوسه سيكون ثابتا :
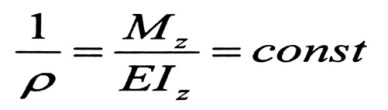(2)
أي أنه لنصف قطر التقوس قيمة ثابتة أيضا ، وهكذا في الانعطاف الصافي فإن الجائز ينحني بشكل دائري .
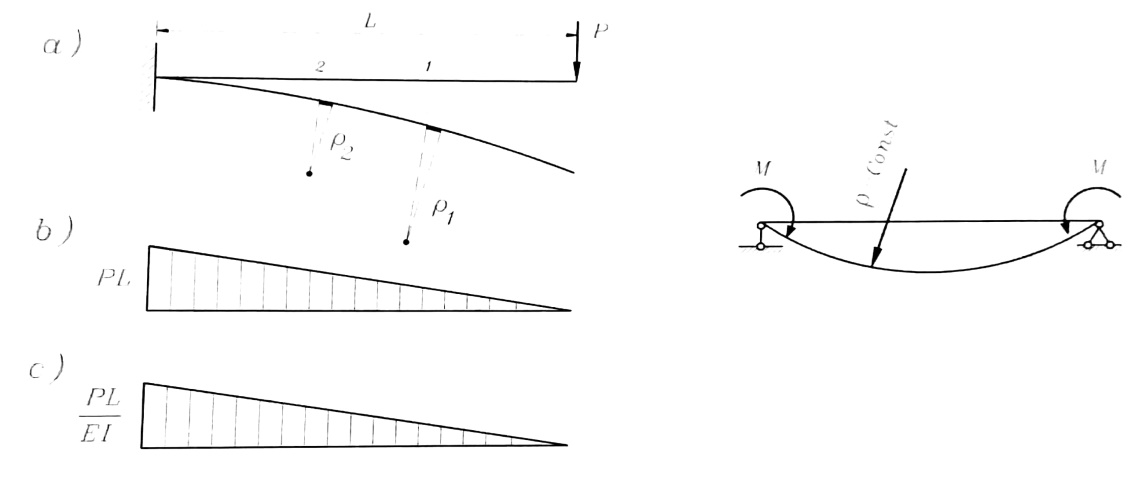
الشكل رقم (1)
لكن في الحالة العامة ، من أجل تحديد السهوم ، لا يمكننا تطبيق قانون تغير التقوس بشكل مباشر ، فنستخدم من منهاج التحليل الرياضي العلاقة الآتية التي تعطينا تقوس الخط المرن :
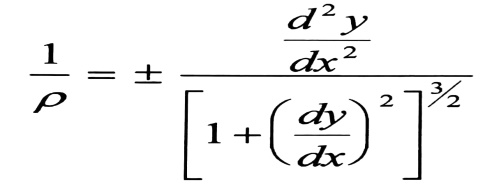(3)
بتعويض قيمة التقوس من العلاقة رقم (2) بالعلاقة رقم (3) ، نحصل على المعادلة التفاضلية لمحور الجائز المنحني أو ما تسمى بمعادلة الخط أو المحور المرن :
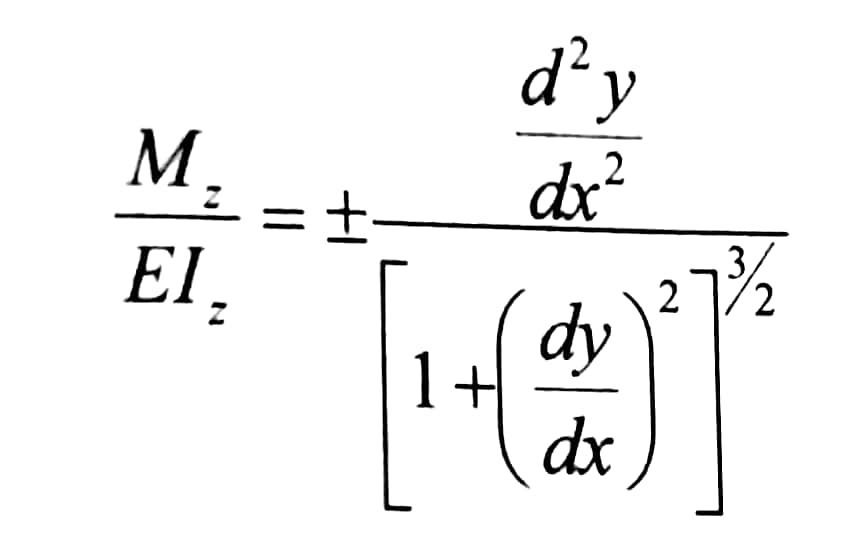(4)
وهي عبارة عن معادلة تفاضلية لا خطية ، دقيقة لمحور الجائز المنحني " الخط المرن " وحلها التفاضلي صعب جدا .
لكن إذا أخذنا بعين الاعتبار بأنه يمكن في معظم المسائل التطبيقية إهمال المقدار 2(dy/dx) لصغره مقارنة بالواحد فنحصل على المعادلة التفاضلية التقريبية التالية :
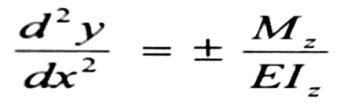(5)
يلاحظ من المعادلة رقم (5) وجود الإشارتين (+ , ‒) لأن إشارة التقوس :
Download eMufeed Android Application Now
