الطريقة العامة للخط المرن (طريقة الشروط الابتدائية)
إذا كان الجائز مؤلفا من عدة مجالات فإن تعيين شكل الخط المرن يصبح صعبا نوعا ما ، إذ أن معادلة كل مجال بعد التكامل تحوي ثابتين فإذا تألف الجائز من n مجالا فيكون لدينا عندئذ n معادلة لعزم الانعطاف وبإجراء التكامل للمرة الأولى فإننا نحصل على n معادلة لزوايا الدوران ، وبالتكامل للمرة الثانية فإننا نحصل على n معادلة للخط المرن . وباعتبار أن كلا من معادلات زوايا الدوران ومعادلات الخط المرن للجائز يحوي (2n) ثابتا للتكامل ، فإنه يلزم حل (2n) معادلة من المعادلات لتعيين (2n) من ثوابت التكامل ، أي أن طريقة التكامل لا تعود مجدية في مثل هذه الحالات ولذلك عندئذ نلجأ إلى استخدام طريقة أخرى هي طريقة الشروط الابتدائية التي بموجبها يمكن الاكتفاء بتعيين ثابتين فقط ، وذلك مهما كان عدد المجالات التي يحويها الجائز ، وذلك باتباع القواعد التالية :
-1 اختيار مبدأ الإحداثيات في الطرف الأيسر .
-2 يتم تكامل أي مقدار ضمن قوس دون تحليل القوس " مبدأ كلابشي "
-3 عندما يخضع الجائز لعزم انعطاف m وأثناء كتابة معادلة العزم في أي مجال منه يؤخذ مقدار العزم m مضروبا بالقوس 0(x‒a) المساوي إلى الواحد .
-4عند كتابة معادلة عزم الانعطاف نأخذ فقط القوى الواقعة على يسار المقطع .
-5 إذا كانت الحمولة الموزعة بانتظام تؤثر على جزء من الجائز فيفترض أن تستمر هذه الحمولة حتى المقطع المعين ، ولكي لا تتغير شروط عمل هذا الجائز يجب إضافة حمولة معاكسة تكون مساوية بالمقدار ومخالفة بالإشارة للحمل الأول .
(الحمولة الممتدة والحمولة المعاكسة مبينة بشكل متقطع على الشكل رقم (1)).
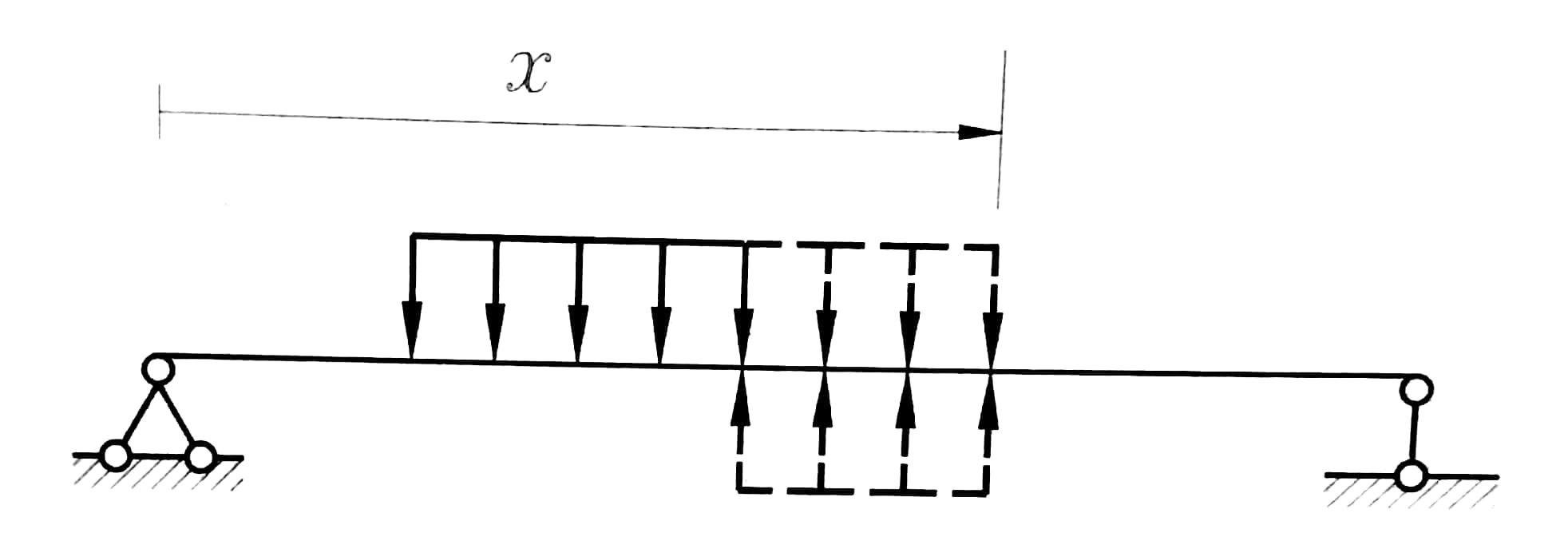
الشكل رقم (1)
لتوضيح هذه الطريقة نفرض أن الجائز المبين بالشكل رقم (2) والمحمل بالحمولات التالية : عزم مركز m ، وقوة p ، وحمولة شدتها q موزعة بصورة منتظمة في مجال ما من الجائز ، بحيث تكون عزوم الانعطاف الناتجة عنها موجبة في مقاطع الجائز المختلفة .
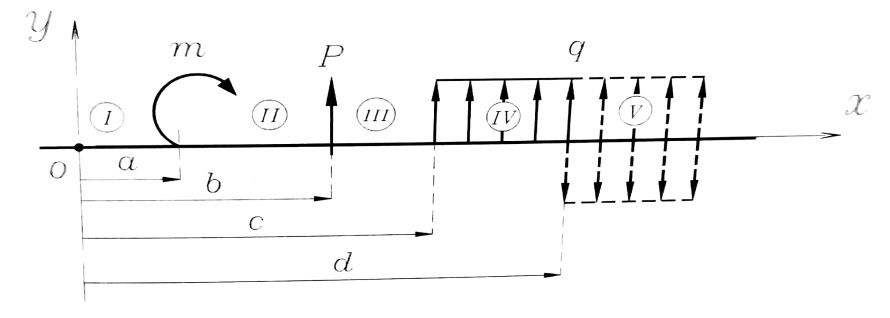
الشكل رقم (2)
نأخذ مبدأ الإحداثيات في النقطة o على يسار الجائز والمحور x موجه نحو اليمين وفق محور الجائز ، والمحور y موجها نحو الأعلى .
إن الجائز مكون من خمسة مجالات ، وسنقوم بتعيين الخصائص والمميزات المختلفة لمعادلة الخط المرن باختلاف أنواع الحمولات الخارجية .
- نكتب معادلات عزوم الانعطاف لكل مجال من المجالات الخمسة المبينة على الشكل رقم (2) :
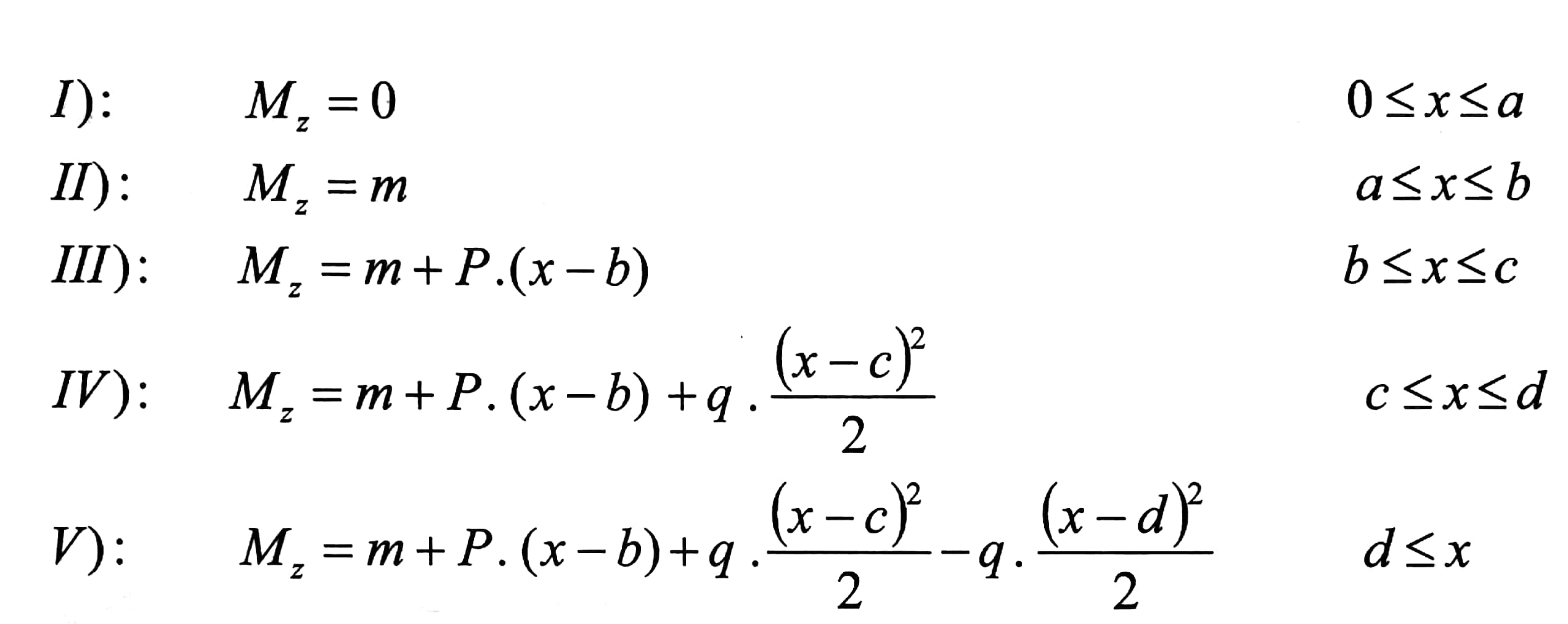
كما نرى معادلة عزم الانعطاف لكل مجال تحتوي على معادلة المجال السابق وتختلف عنه بإضافة حد جديد .
عند الانتقال من المجال الرابع إلى الخامس ، وحفاظا على هذا التتابع ، تمدد الحمولة الموزعة بانتظام المؤثرة في المجال الرابع كما هو مبين بخط متقطع على المجال الخامس ، بالوقت ذاته تضاف إلى المجال الخامس حمولة معاكسة سالبة وموزعة بانتظام شدتها q .
نكامل المعادلات الناتجة مرة واحدة دون فك الأقواس .
ولحفظ نمط واحد للعلاقات الناتجة نكتب العزم m بالشكل m(x ‒ a)0 في علاقات العزوم السابقة ، وهذا مايؤثر فقط على مقدار الثابت Ci .
بالنتيجة نحصل على المعادلات التالية لميل المماس للخط المرن :
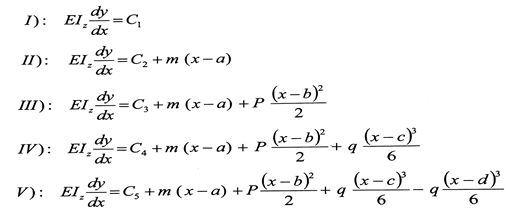
المقادير الثابتة Ci تختار بحيث يكون الانتقال من مجال إلى آخر مستمرا دون انكسار ، إذن عندما :
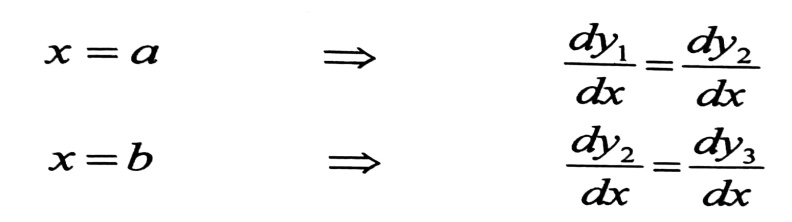
وهكذا وبما أن صلابة الجائز واحدة ، إذن :

إن زاوية ميل مماس الخط المرن 0ϕ في بداية الإحداثيات تتعين من معادلة المجال الأول :
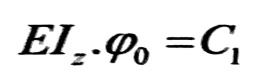
بمكاملة العلاقات السابقة مرة ثانية ، نجد :









