حساب الجوائز غير المقررة استاتيكيا من الدرجة الثانية 

   حساب الجوائز غير المقررة استاتيكيا من الدرجة الثانية

لحساب مثل هذه الجوائز  يلزمنا معادلتا تشوه إضافيتان زيادة على معادلات التوازن الثلاثة ، وتعتبر المعادلات كلها مشتركة ، ويوضح المثال التالي طريقة حل مثل هذه الجوائز :

مثال :

ليكن لدينا جائز بفتحتين موثوق من نهايته اليسرى ، ومحمل بحمولة مركزة P بمنتصف الفتحة اليمنى كما هو واضح بالشكل رقم (1-a) ، صلابة الجائز على الانعطاف بالفتحة اليمنى EI_Z واليسرى 2EI_Z .

والمطلوب :

-1 رسم مخططات M_Z و Q_y .

-2 تعيين ردود الأفعال في المساند .

-3 إيجاد السهم وزاوية الدوران في النقطة k منتصف الفتحة اليسرى .

الحل :

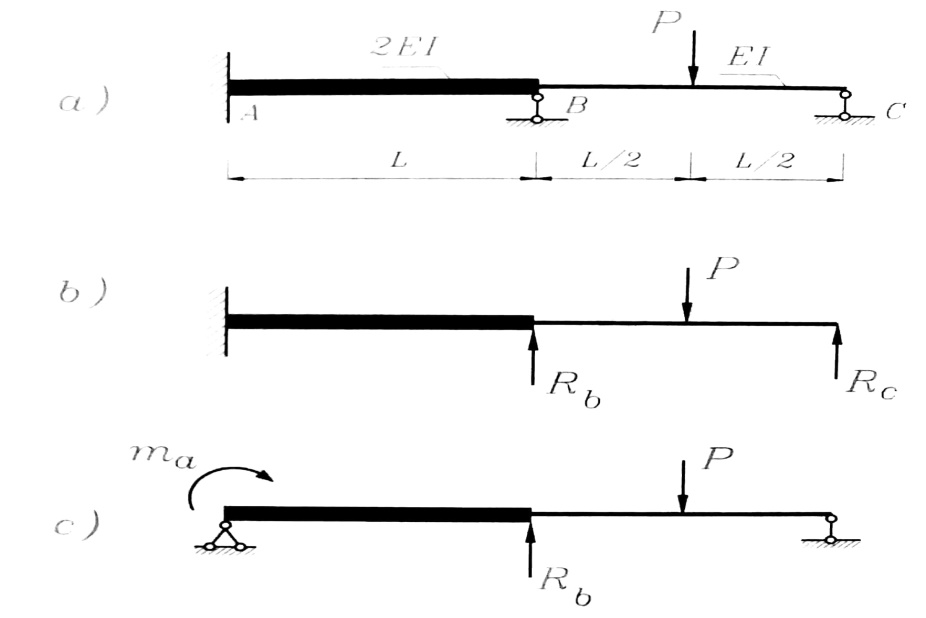
الشكل رقم (2)

-1 إن الجائز غير مقرر من الدرجة الثانية ، لأن عدد ردود الأفعال فيه خمسة ، ولحله لا بد من اختيار الجملة الأساسية ، ثم تشكيل معادلتي التشوه الإضافيتين ، إن اختيار الجملة الأساسية يمكن أن يتم بشكلين :

- بالشكل الأول نأخذ ردود الأفعال المجهولة في المسندين B,C .

- بالشكل الثاني نأخذ العزم في الوثاقة ورد الفعل في النقطة B .

لتعيين المجاهيل بالشكل الأول نستعمل شرط انعدام السهم في المسندين .

y_B = 0  ;  y_c = 0

أما لتعيين المجاهيل بالشكل الثاني فنستعمل شرط انعدام زاوية الدوران في الوثاقة ، والسهم في المسند B .

ϕ_A =0  ; y_B = 0

وباعتبار المجموعتين الرئيستين بسيطتان إلى حد ما ، لذا من الصعب إعطاء الأفضلية لإحداهما .

لندرس الشكل الأول : إن الشكل النهائي لمعادلات التوازن هو :

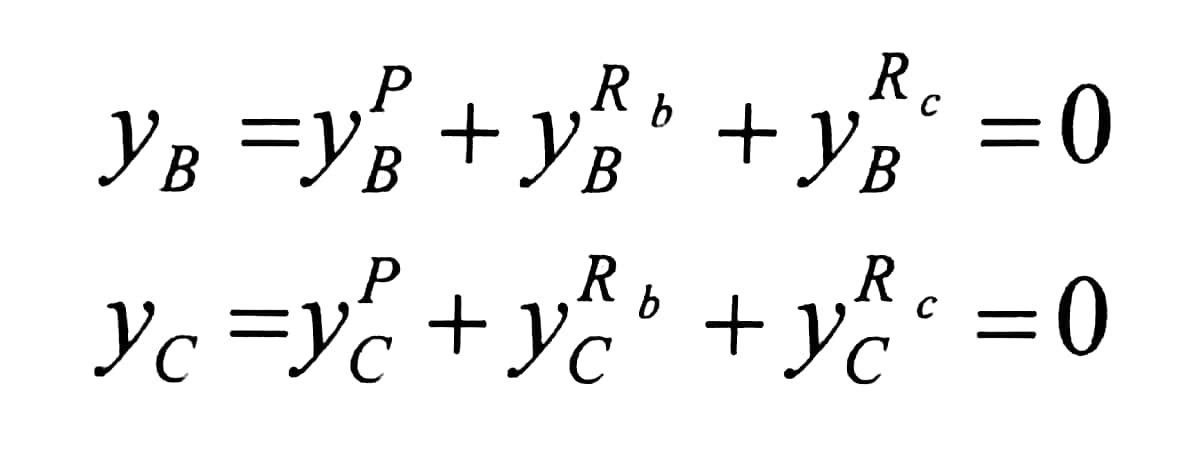 (1)

حيث :

y_B^P ; y_c^P  : سهمي النقطتين B , C في الجملة الرئيسية من تأثير الحمولة الخارجية P .

y_B^Rb ; y_B^RC : سهمي النقطة B ، من تأثير المجهولين R_b , R_c .

y_c^Rb ; y_c^RC : سهمي النقطة C ، من تأثير المجهولين R_b , R_c .

لتعيين الانتقالات الواردة بالمعادلة رقم (1) نستعمل طريقة الجائز المرافق . ويبين الشكل رقم (2) مخطط العزوم للجملة الرئيسية تحت تأثير كل من P ، R_c ، R_b والجوائز المرافقة المحملة بالحمولة المرنة التخيلية .

(1-  حساب y_B^P ; y_c^P نحسبها من شرط مساواة السهم في الجائز الحقيقي بالعزم في الجائز المرافق :

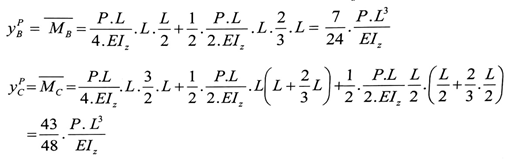
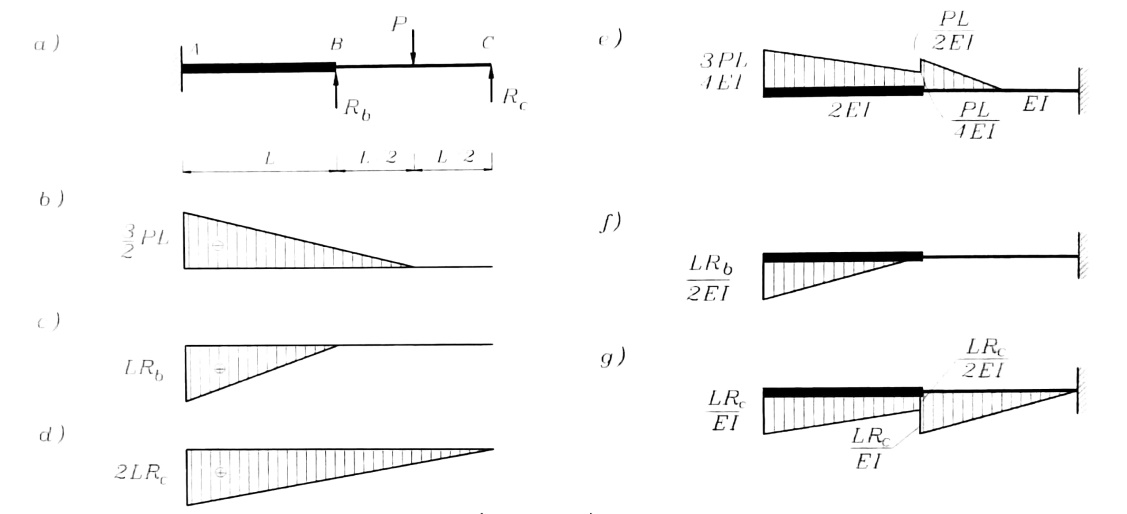
الشكل رقم (2)

(2- حساب y_B^Rb ، y_c^RC (الشكل رقم 2-f) :