تتعلق دقة نتائج حساب التكاملات المحددة عند استخدام قاعدة سيمبسون وشبه المنحرف، بدرجة كبيرة بخصائص المنحني المعطى وبكثافة التقسيم، فكلما ازدادت كثافة التقسيم قل اختلاف قطاعات المنحني المحيط بالمساحة المطلوبة عن خط المستقيم أو التوابع المنحنية البديلة وأيضا كلما كانت العلاقات المستخدمة في الحسابات الرقمية للتكاملات تستند إلى توابع لمنحني من درجات اعلى ازدادت دقة النتائج، لهذا السبب تعتبر عادة قاعدة تشيبشف من أدق الطرق ثم تأتي قاعدة سيمبسون وأخيراً قاعدة شبه المنحرف.
عملياً لرفع دقة الحسابات الرقمية عند حساب العناصر الهندسية لبدن السفينة تستخدم الطرق التالية:
استخدام إحداثيات راسية إضافية:
للحصول على نتائج دقيقة للتكاملات الرقمية عند ظهور انحناء شديد في المنحني المدروس عند نهايات مجال التكامل، غالباً ما تستخدم إحداثيات رأسية إضافية كما في الشكل التالي، في هذه الحالة على سبيل المثال تقسم القطاعات 8-9 و 9-10 مناصفة باستخدام إحداثيات رأسية إضافية تقع في منتصف المسافة بين الإحداثيات الرأسية الأساسية، ينبغي الإشارة إلى أن إدخال إحداثيات رأسية إضافية يؤدي الى حدوث تغير في قيم معاملات التكامل المستخدمة في الحساب الرقمي للمساحات، لتوضيح ذلك سيتم حساب المساحة أسفل المنحني المبين في الشكل باستخدام قاعدة شبه المنحرف:
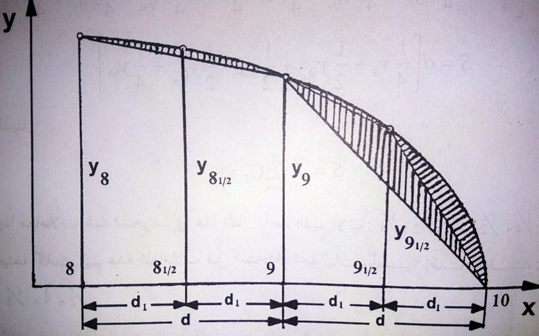
قاعدة شبه المنحرف:
قم بتنزيل تطبيق eMufeed Android الآن
