الشكل الاقتصادي للمقطع العرضي للجوائز العاملة على الانعطاف

​

 الشكل الاقتصادي للمقطع العرضي للجوائز العاملة على الانعطاف

إن توزع الإجهادات على نقاط المقطع العرضي في حالة الانعطاف تمكننا من صياغة بعض الاستنتاجات عن الشكل الاقتصادي للمقطع .

تتوزع الإجهادات الناظمية على المقطع العرضي بشكل غير منتظم ولذلك فإن القسم "من مادة الجائز " الواقع بجوار المحور المحايد يكون غير مجهد بشكل عام . لذلك لتخفيف وزن الجائز والاقتصاد في المادة يجب اختيار شكل المقطع العرضي بصورة يكون فيها أكبر قسم من المادة بعيدا عن المحور المحايد .

فمن وجهة النظر هذه يكون المقطع المؤلف من مستطيلين ضيقين ، الشكل رقم (1) ، مقطعا مثاليا . ومن أشكال المقاطع التي نصادفها في الحياة العملية والقريبة من المقطع المثالي يعتبر المقطع بشكل I .

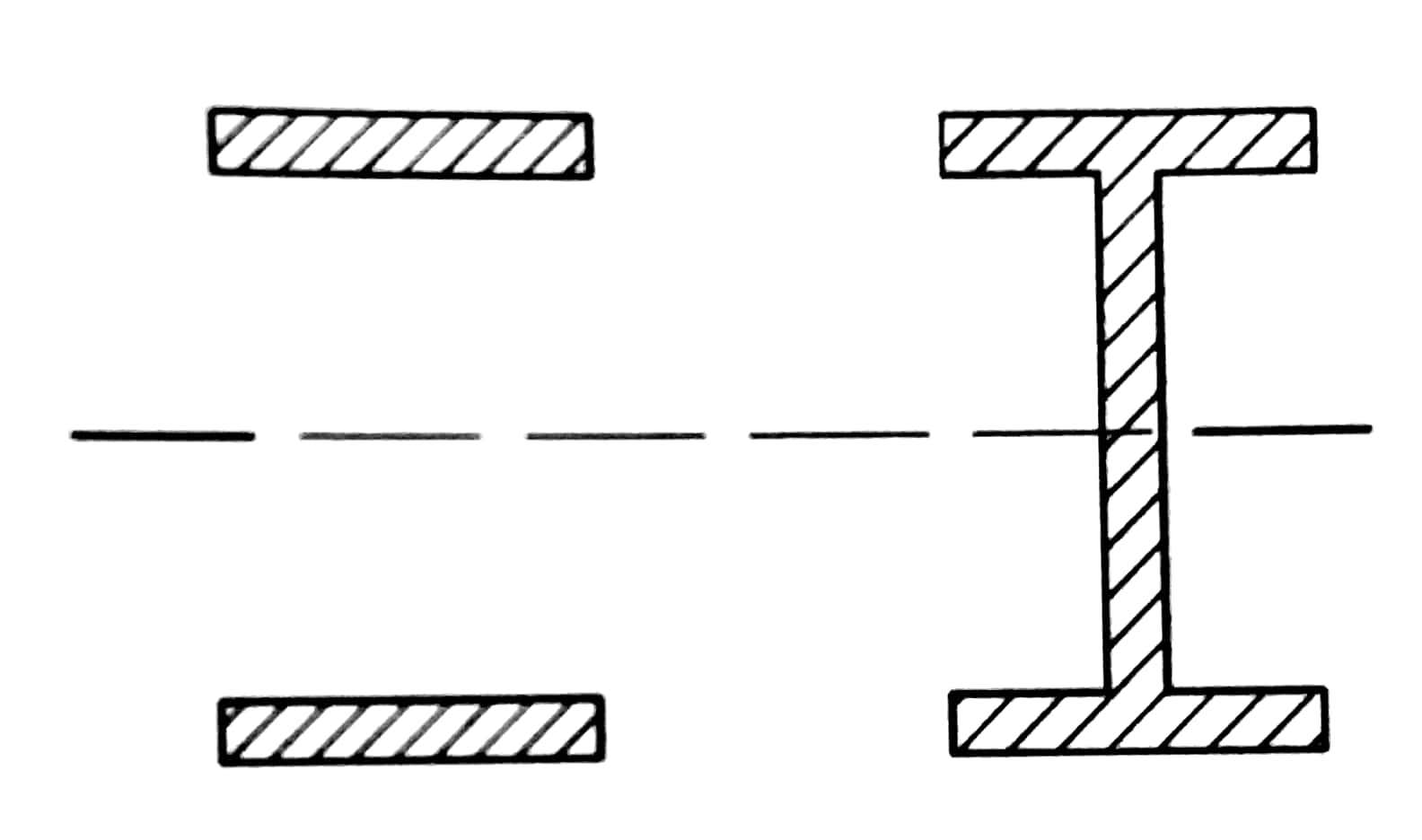
الشكل رقم (1)

إن أكبر عزم يمكن بأمان أن يتحمله مقطع يتناسب مع عزمه المقاوم :

كما أن حجم المادة يتناسب مع مساحة المقطع A ، وهكذا كلما كانت النسبة W_c/A كبيرة كلما كان العزم الذي يمكن أن يتحمله المقطع كبيرا وذلك باعتبار أن A معطاة ، وكان حجم المادة اللازم لصنع الجائز أقل من أجل عزم انعطاف معطى . ولهذا فإن النسبة W_Z/A يمكن اعتبارها صفة مميزة للمقطع .

فمثلا من أجل A = const ، يكون لكل مقطع من المقاطع المبينة على الشكل رقم (2) عزم مقاوم مختلف .

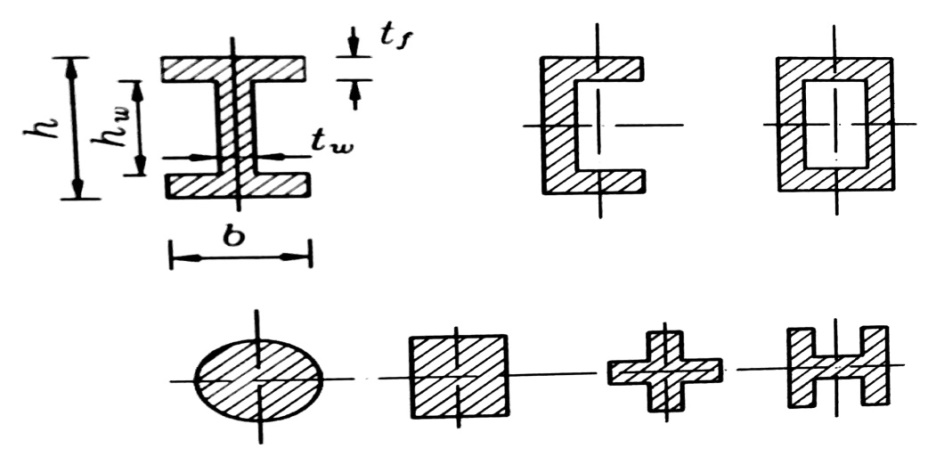
الشكل رقم (2)

تقاس اقتصادية المقطع بالمعامل :

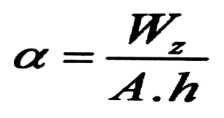
حيث :

A : مساحة المقطع .

h : ارتفاع المقطع (البعد العمودي على المحور المحايد) .

قيمة العامل α لبعض المقاطع معطاة بالجدول التالي :

إذن بغض النظر عن المتطلبات التكنولوجية المتعلقة بشكل المقطع لعنصر ما ، يعتبر مقطعا اقتصاديا ذلك الذي يؤمن المتانة الكافية وكان له أخف وزن (أي أقل مساحة) .

كما أن وضعية المقطع بالنسبة لمستوي تأثير القوى تعتبر ذات أهمية كبيرة . حيث يجب أن تكون وضعية المقطع بشكل ينطبق فيه المحور المحايد مع محور العطالة الأعظمي .

وبالتالي فإن اختيار المقطع الدائري على الانعطاف هو اختيار غير منطقي إذا لم تكن هناك متطلبات تصميمية وتكنولوجية لذلك .

- إن ما ذكر صحيح من أجل أي جائز ذي مقطع ثابت يعمل على الانعطاف المستوي ومصنوع من مادة تعمل على الشد كعملها على الضغط : [σ_t] = [σ_c] .

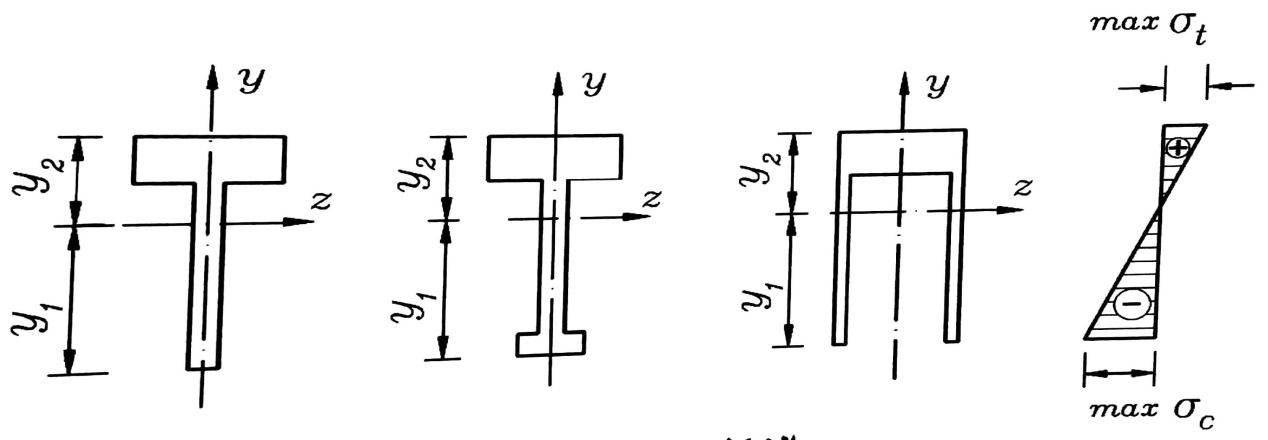
الشكل رقم (3)

أما عندما يكون الجائز مصنوعا من مادة هشة ([σ_t] ≠ [σ_c]) فإن الاستنتاجات السابقة تفقد قيمتها ، وفي هذه الحالة يكون غير منطقي أن نختار المقطع بحيث يكون المحور المحايد هو محور تناظر له . ويكون منطقيا ذلك المقطع الذي يكون بالنسبة له الإجهاد الأعظمي في القسم الواقع في حالة الشد أصغر بكثير  من الإجهاد الأعظمي في القسم الواقع في حالة الضغط . ويتحقق ذلك باختيار شكل المقطع بحيث يكون المحور المحايد مزاحا إلى جهة الجزء الواقع في حالة الشد ، مثل ذلك مبين على الشكل رقم (3) .

مثال :

عين نسبة الاقتصاد في المعدن إذا بدلنا عنصرا يعمل على الانعطاف مقطعه العرضي دائري أصم قطره D₁ بمقطع دائري مجوف نسبة قطريه C = d₂/D₂ = 0.9  ، بحيث تبقى شروط العمل نفسها ، الشكل رقم (4) .

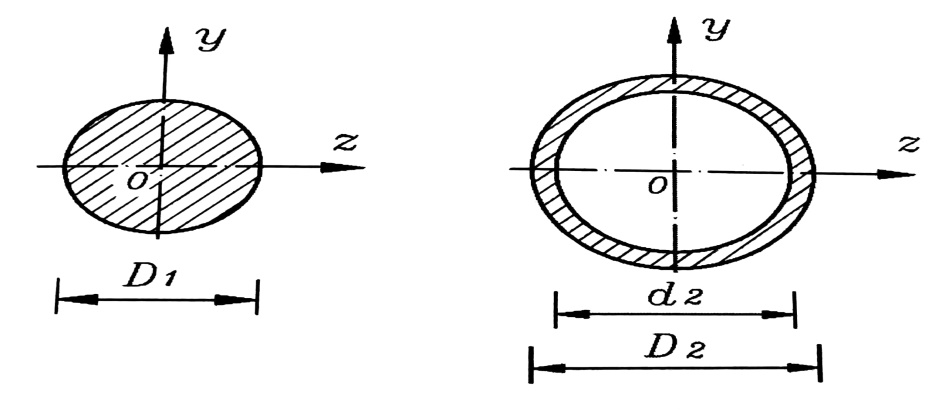
الشكل رقم (4)

الحل :

إن العزم المقاوم للمقطع الدائري الأصم يتعين بالعلاقة :

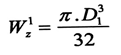
أما للمقطع المجوف فيتعين بالعلاقة :

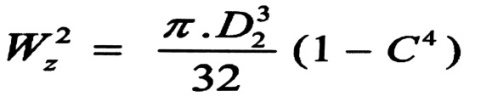
من شرط تساوي المتانة ، يكون :

​