فرضيات المتانة  

  فرضيات المتانة  

استنادا إلى تجارب مخبرية على الشد أو الضغط المركزي تحت تأثير حمولة ستاتيكية ، تعين الحالة الخطرة أو الحالة الحدية للمواد ، والتي تصف بدء الخضوع المترافق مع تشوهات لدنة إضافية كبيرة أو ظهور شقوق دالة على بدء التحطم أو الانكسار .

إن قيمة الإجهادات الناظمية لحظة بدء الحالة الحدية تساوي حد الخضوع σ_y للمواد اللدنة ، وتساوي حد المتانة أو المقاومة المؤقتة σ_u للمواد الهشة أما بالنسبة للمواد الواقعة بين اللدنة والهشة فقيمة هذه الإجهادات تفرض بشكل اصطلاحي وتسمى بحد المرونة الاصطلاحي .

كما أن المادة نفسها يمكن أن تسلك سلوكا لدنا وسلوكا هشا عند حالات إجهادية مختلفة وفي ظروف اختبار مختلفة (كالحرارة في الوسط المحيط وسرعة التشوه وغير ذلك ).

ويعد الحديد الصب مثالا على المواد الهشة ، فمقاومته للانقطاع أقل من مقاومته للقص ، ولهذا فإن فقدان التماسك بين ذرات أجزائه يحصل عند ظهور التشوهات المتبقية ويحدث انهياره بسبب الانقطاع . أما الفولاذ اللين فهو من المواد اللدنة ، التي تكون مقاومتها للقص في البداية أقل من مقاومتها للانقطاع ويحدث قص لذراتها البلورية بسبب ظهور التشوهات المتبقية فيها و مع ظهور تلك التشوهات تزداد مقاومتها للقص ، وبالتالي تستعيد المادة قابليتها لمقاومة الشد " تتقوى " ، أما التحطم النهائي للمادة فترافقه تشوهات لدنة عالية .

وبهذا الشكل نستنتج أن متانة المواد الواقعة في الحالة الهشة تصف قيمة مقاومتها للقص عند تشكل تشوهات لدنة .

ويعد الجسم في حالة حدية إذا وقعت إحدى نقاطه في حالة حدية ، وتدعى النقطة التي تظهر حولها الحالة الخطرة للمادة نتيجة أية زيادة في الحمولة بالنقطة الخطرة أو الحدية .

توجد وجهات نظر مختلفة حول الأسباب المؤدية للحالة الخطرة ، فبعضهم يرى أنها تحدث نتيجة وصول الإجهادات الناظمية الشادة إلى قيمتها الحدية ، وبالتالي ينبغي أن نحد من قيمة تلك الإجهادات ، والبعض الآخر يرى أن سبب ظهور الحالة الخطرة هو التشوهات الخطية العظمى ولذلك يجب أن نحد من قيمها ، وآخرون أيضا يطالبون بالحد من قيم الإجهادات المماسية أو طاقة التشوه الكامنة وذلك لكونها سببا لحدوث الحالة الخطرة .

ففي حال كون سببها هو الإجهادات الناظمية الشادة فإن النقطة الخطرة هي النقطة التي يظهر عندها أكبر  إجهاد شد ، أما إذا كان سبب حدوثها هو الإجهادات المماسية فعند ذلك تكون النقطة الخطرة هي تلك النقطة الموافقة لظهور أكبر إجهادات مماسية وهكذا ... ، ولذلك فإن وضع النقطة الخطرة يتعلق بما نعتبره سببا لحدوث الحالة الخطرة .

وبما أنه لا يسمح للمادة بالوصول إلى الحالة الخطرة ، لذا فحساب المواد على المتانة يقصد به الحالة المسموح  بها للمادة والتي توافق الحمولة الناتجة من تقسيم الحمولة المسببة للخطر على عامل أمان أكبر من الواحد .

ففي الحالة الإجهادية المحورية نرى أن السبب الحقيقي لحدوث الحالة الخطرة التي تسبب انهيار المادة ليس أي قيمة عملية في الحساب على المتانة وذلك لكون الإجهادات المسموح بها محددة دائما من النتائج المخبرية للمادة .

أما في الحالة الإجهادية المستوية والحجمية فيمكن أن يحصل تشوه المادة وتحطمها نتيجة تأثير اثنين أو ثلاثة إجهادات رئيسية ، كما يمكن أن يحصل من أجل أي نسب بين هذه الإجهادات وعدد هذه الحالات كبير جدا ، وبالتالي عدد التجارب التي كان من اللازم إجراؤها من أجل تحديد القيم الحدية للإجهادات كذلك كبير جدا ، كما أن إمكانية إجراء مثل هذه التجارب على درجة من التعقيد وغير ممكن عمليا . لذلك كان من الضروري وضع طريقة مساعدة تساعد على تقدير درجة خطورة أي حالة إجهادية للمادة بالاستناد إلى النتائج التجريبية لحالة الشد (ضغط) البسيط .

وهكذا فإن نتائج التجارب على الحالة الإجهادية المحورية للشد أو الضغط تصبح معيارا للمتانة تستخدمه لتقدير المتانة في الحالة المستوية و الحجمية ، ومن أجل ذلك يدخل مفهوم الإجهاد المكافئ σ_eq .

- ويكتب شرط المتانة لأي حالة إجهادية : σ_eq = f (σ₁ ; σ₂ ; σ₃) .

أو بالشكل :

ومن أجل حل المسألة السابقة لا بد من إيجاد علاقة بين الإجهادات الرئيسية وما يكافئها من حالة الشد أو الضغط .إن إيجاد مثل هذه العلاقة ممكن فيما لو عرف السبب المشترك (للحالتين) الذي يؤدي إلى تحطم المادة أو  إلى لوصول إلى الحالة الإجهادية الحدية .

إلا أن تعيين السبب الحقيقي لتحطم المادة مسألة على غاية من التعقيد وغير مدروسة بشكل كاف حتى وقتنا الحاضر . وهذا السبب أدى لوجود عدة فرضيات للمتانة وعدم وجود فرضية واحدة شاملة .

- إن نتائج فرضيات المتانة المختلفة غالبا ما تعطي نتائج متناقضة ولا تتطابق مع التجارب ، ولذلك فإنه لكل حالة خاصة متعلقة بنوعية المادة والحالة الإجهادية في النقطة الخطرة ، يجب أن نجري الحساب وفقا لفرضية المتانة التي تعطي دقة أكثر وتكون قريبة من النتائج التجريبية .

- يعبر عن العلاقات الحسابية لمختلف فرضيات المتانة وللحالة الإجهادية للمادة بدلالة الإجهادات الرئيسية : σ₁ , σ₂ , σ₃ ، حيث : σ₁ ≥ σ₂ ≥ σ₃ .

فرضية المتانة الأولى :

وتدعى فرضية الإجهادات الناظمية الأعظمية ، وقد وضع أساسها العالم غاليليه وتنص على أن المادة تتحطم نتيجة الإجهادات الناظمية الأعظمية ولا يتعلق انهيارها بطبيعة الحالة الإجهادية ، لذلك في حال حساب المتانة يجب أن نحد من قيمة الإجهاد الناظمي الأعظمي والأصغري (الشاد والضاغط) بحيث لا تزيد عن قيم الإجهاد المسموح بها والمعينة تجريبيا لحالة إجهادية محورية شادة أو ضاغطة .

في حال كون الإجهاد المسموح به للمادة واحدا في حالتي الشد والضغط (المواد اللدنة) ، فإن شرط المتانة حسب فرضية المتانة هذه هو التالي :

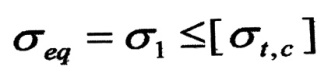  (2)

وفي حال كون الإجهاد المسموح به في حالة الشد مختلفا عنه في حالة الضغط (المواد الهشة ) فإن شرط المتانة عندئذ :

حيث : [σ_t]               و [σ_c] – توافق الإجهادات المسموح بها على الشد والضغط على التوالي .

- من مساوئ هذه الفرضية أنها لا تأخذ بعين الاعتبار دور الإجهادات الرئيسية ₂σ و σ₃ أثناء حساب متانة المادة لدنة كانت أم هشة .

وبالتالي فهي لا تبين بأن متانة المادة الخاضعة لإجهادات ضاغطة متساوية وفق ثلاثة محاور هي أكبر بكثير من متانتها على الضغط البسيط وفق محور وحيد . لكنها تعطي نتائج قريبة من المعطيات التجريبيبة للمواد الهشة (الحديد الصب ، الحجر ، ...).

فرضية المتانة الثانية :

وتدعى بفرضية التشوهات الخطية العظمى ، وحسب هذه الفرضية تحدث الحالة الخطرة للمادة عندما تصل قيمة التشوهات الخطية النسبية العظمى إلى القيمة الخطرة . لذلك فمن أجل ضمان متانة المادة يجب أن لا تزيد التشوهات النسبية العظمى عن التشوهات النسبية المسموح بها [Ꜫ] والمعينة تجريبيا لحالة إجهادية محورية . وبذلك نرى أن شرط المتانة حسب هذه الفرضية يأخذ الشكل التالي :

وإذا افترضنا أن المادة تخضع لقانون هوك حتى لحظة حدوث الانكسار (نستطيع أن نفترض ذلك للمواد الهشة فقط) فيمكننا الانتقال من التشوهات إلى الإجهادات مستخدمين قانون هوك العام .

وتبعا للقاعدة المتبعة بالنسبة لإشارة الإجهادات الرئيسية (σ₁ ≥ σ₂ ≥ σ₃) ستكون القاعدة المتبعة للتشوهات الرئيسية الثلاثة أيضا (Ꜫ₁ ≥ Ꜫ₂ ≥ Ꜫ₃) ، وبالتالي :

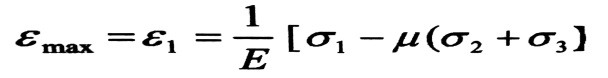   (4)

إذا كانت قيمة الإجهادات المسموح بها على الشد أو الضغط البسيط هي [σ] ، فإنه وفقا لقانون هوك تكون القيمة المسموح بها للتشوه الخطي هي :

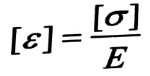
ولذلك نستطيع أن نعبر عن الشرط في المعادلة رقم (3) بدلالة الإجهادات المعطاة حسب العلاقة رقم (4) بالشكل التالي :

σ_eq = σ₁ - µ(σ₂ + σ₃) ≤ [σ]  (5)

حيث : σ_eq : هو الإجهاد المكافئ .

إن معطيات التجارب لا تؤكد صحة هذه الفرضية أيضا . ففي الواقع وحسب هذه الفرضية يجب أن يتحمل العنصر المعرض للشد باتجاهين قوة أكبر فيما لو كان معرضا للشد باتجاه محوري وحيد، ولكن التجارب المخبرية لا تؤكد صحة ذلك .

فرضية المتانة الثالثة :

وتدعى هذه الفرضية بفرضية الإجهادات المماسية الأعظمية ، حيث السبب الرئيسي لظهور الحالة الخطرة (حد الخضوع)للمادة هو بلوغ الإجهادات المماسية قيمتها الأعظمية .