فرضية مور للمتانة
إن هذه الفرضية مبينة على افتراض أن متانة المادلة في الحالة الإجهادية العامة تتعلق بشكل رئيس بقيمة وإشارة أكبر إجهاد ناظمي (σ1) وأصغر إجهاد ناظمي (σ3)، أما الإجهاد (σ2) فيؤثر قليلاً على متانة المادة 15-10% لذلك يمكن إهماله. وانطلاقاً من هذه الفرضية يمكن تمثيل أية حالة إجهادية بواسطة دائرة (دائرة مور) يتم إنشائها بواسطة الإجهادات σ3,σ1، الشكل رقم (1).
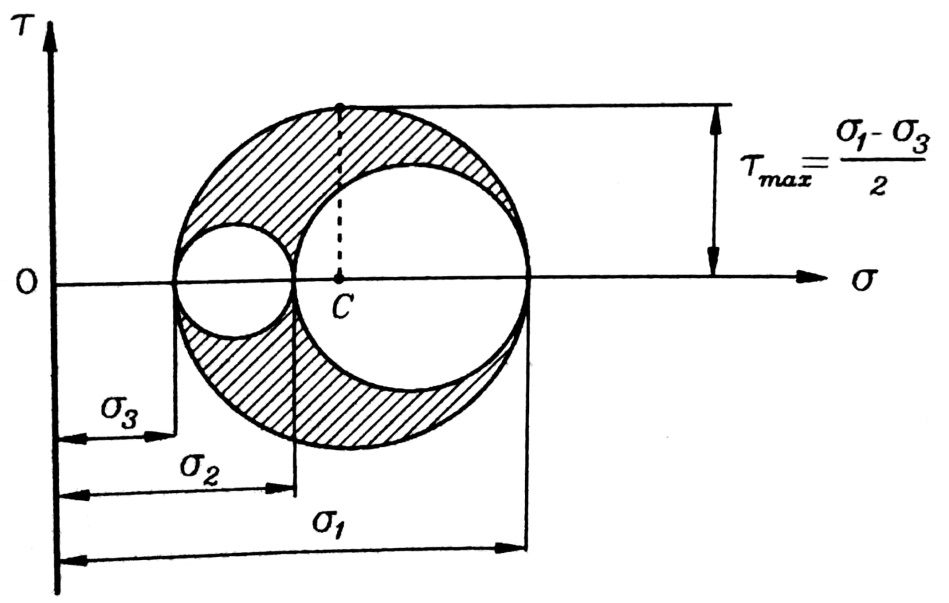
الشكل رقم (1)
عندما تشكل الإجهادات σ3 , σ1 الحالة الإجهادية الحدية، فإن الدائرة الممثلة بواسطة هذه الإجهادات تسمى دائرة حدية. وبتغيير الحالة الإجهادية تتغير الإجهادات σ3 , σ1. وبالتالي يمكننا الحصول على مجموعة دوائر حدية للمادة المدروسة، كما هو مبين في الشكل رقم ((2.
تبين التجربة أنه كلما انتقلنا من مجال الشد باتجاه الضغط فإن قطر دائرة مور يزداد وبالتالي تزداد متانة المادة. إن مغلف مجموعة دوائر مور الحدية، يمثل الحالة الإجهادية الحدية للمادة على الشد و الضغط ![]() ويتعلق بصفات المادة الميكانيكة، وبالتالي يحدد مجال متانة تلك المادة.
ويتعلق بصفات المادة الميكانيكة، وبالتالي يحدد مجال متانة تلك المادة.
إن النقطة C توافق حالة الشد المنتظم في جميع الاتجاهات، ونرى أن مغلف الدوائر الحدية يبقى مفتوحاً من الجهة اليسرى في حالة الضغط المنتظم في كافة الاتجاهات، ويفسر ذلك بأن المادة تستطيع أن تتحمل إجهادات كبيرة.
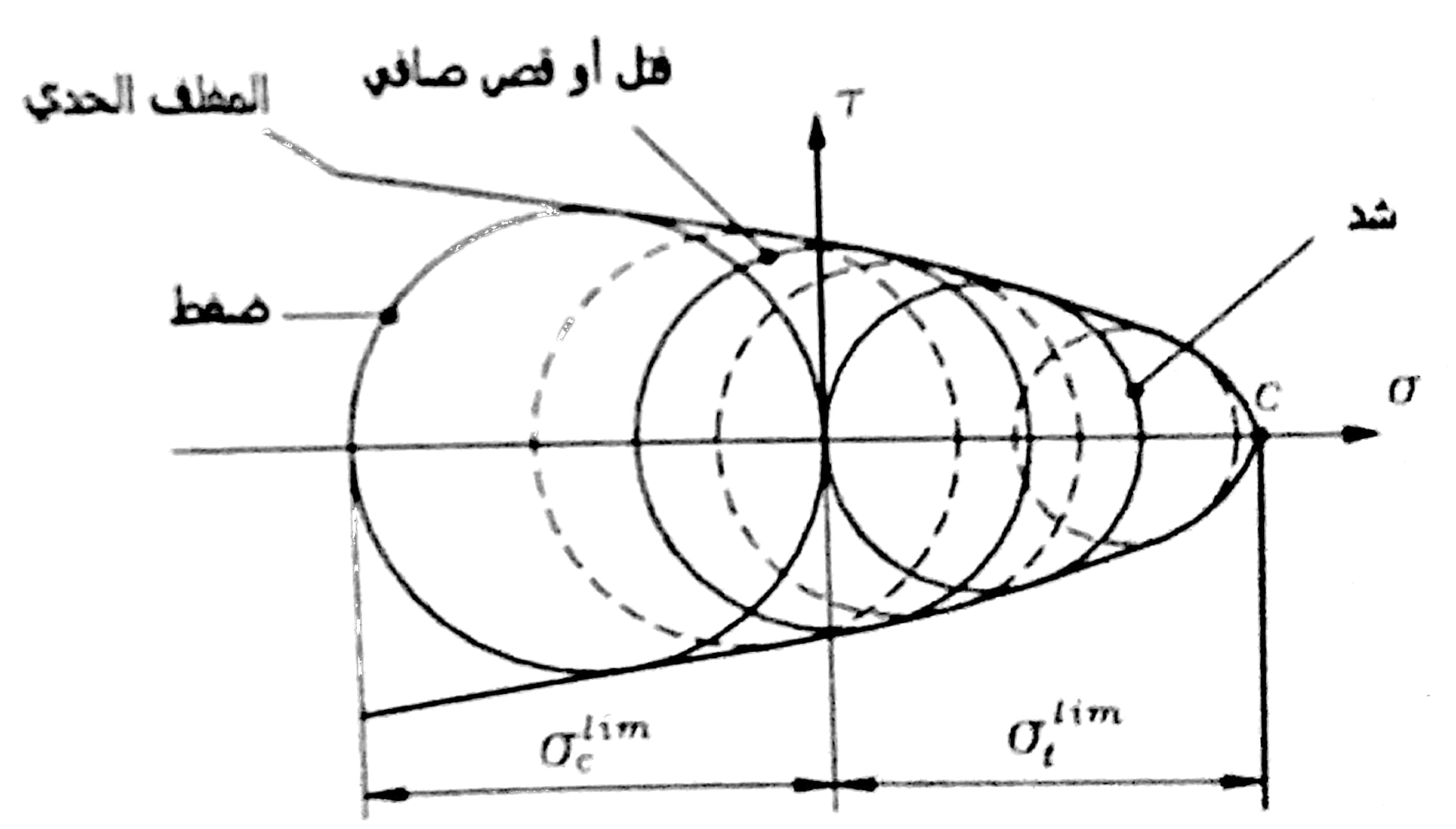
الشكل رقم (2)
إذا كان المغلف الحدي موجوداً فإن عملية التحقق من متانة مادة تكون بغاية السهولة وذلك عن طريق رسم دائرة مور الموافقة للحالة الإجهادية المعطاة بدلالة (σ3,σ1)، فإذا مست تلك الدائرة للمغلف الحدي فهذا يعني أن الحالة الإجهادية للمادة هي حالة حدية.
أما إذا تجاوزته فهذا يعني أن الحالة الإجهادية للمادة زادت عن الحدية مما سيؤدي إلى انهيار المادة أو دخولها ضمن مجال اللدونة.
أما إذا وقعت تلك الدائرة ضمن المغلف الحدي فإن متانة المادة تكون محققة، وإذا قمنا في هذه الحلة بتكبير مناسب لدائرة مور الممثلة للحالة المدروسة حتى تصبح مماسة للمغلف الحدي فإن عدد المرات التي تزداد بها الإجهادات (σ3,σ1) هو عبارة عن عامل الأمان n.









