التشوه الحجمي النسبي

 التشوه الحجمي النسبي

يتغير حجم الجسم المرن نتيجة تطبيق الحمولات الخارجية عليه وبالطبع إذا أخذنا مكعبا أبعاده 1 [cm] × 1  ×1 . فإن حجمه قبل التشوه V_O = 1 [cm³ ] ، أما حجمه بعد التشوه فيساوي :

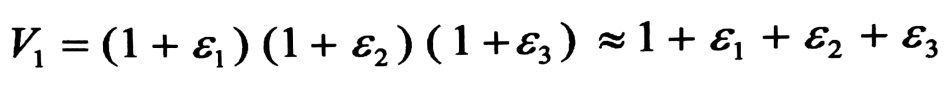
(إن نواتج ضرب Ꜫ هي مقادير متناهية في الصغر بمقارنتها مع Ꜫ نفسها ، ولذلك فإننا نهملها ) .

إن التشوه الحجمي النسبي _VꜪ هو :

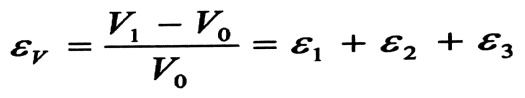
ونعوض هنا عن قيم Ꜫ₁ , Ꜫ₂ , Ꜫ₃ ، من العلاقة رقم ((5) من مقال قانون هوك المعمم ) فنحصل على :

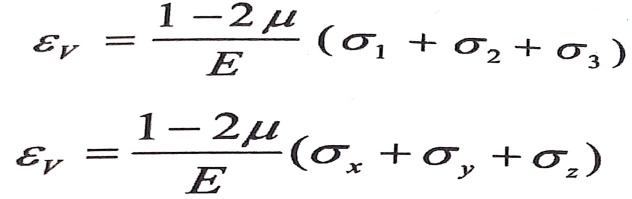
ونستنتج من العلاقتين السابقتين إن معامل بواسون µ لا يمكن أن يكون أكبر من 0.5 . وبالفعل ، فإن الحجم لا يمكن أن يتناقص في حالة الشد الحجمي ، أي أن Ꜫ_V موجب ، وهذا ممكن فقط عندما يكون 1 – 2 µ ≥ 0 ، لأن الإجهادات الرئيسية في هذه الحالة موجبة (σ₁ ≥ σ₂ ≥ σ₃ > 0) .

ملاحظة :

إن العلاقات المرقمة من (1) إلى (7) (من مقال قانون هوك المعمم حتى هذا المقال ) تبقى صحيحة أيضا حتى عندما تؤثر الإجهادات المماسية على الساحات ، أي ليس فقط من أجل حالة إجهادية حجمية رئيسية بل أيضا من أجل حالة إجهادية حجمية عامة . وهذا ينتج عن كون التشوهات الخطية لا تعتمد على الإجهادات المماسية .

مثال (1) :

يراد تحديد الإجهادات σ₁ و ₂σ إذا كانت التشوهات النسبية في هذه الاتجاهات تساوي Ꜫ₁ = 0.001 ، Ꜫ₂ = - 0.0008 ، ومعامل بواسون يساوي  µ = 0.3 ، ومعامل المرونة الطولي يساوي E = 2. 10⁶ Kgf /cm² .

الحل :

من العلاقة رقم (3) لدينا :

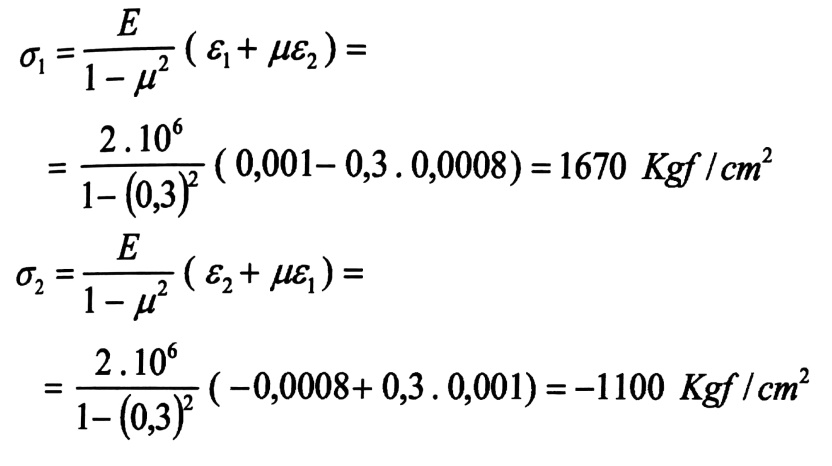
مثال (2) :

دائرة قطرها D = 30 cm ، تم إلصاقها على صفيحة من الفولاذ الطري ، وبعد تعريضها للإجهادات المبينة في الشكل تحولت الدائرة إلى قطع ناقص ، الشكل رقم (1-a) والمطلوب :

- حساب طول كل من محوري القطع (الأعظمي والأصغري) وحساب اتجاههما .

- بفرض أنه يراد إلصاق مربع طول ضلعه A= 30 cm على الصفيحة بشرط أن تبقى أضلاعه متعامدة بعد التشوه ، المطلوب تعيين ميل أحد أضلاعه ، ليتحقق الشرط المطلوب ، الشكل رقم (1-b) ، وحساب أطوال أضلاعه بعد التشوه .

علما أن :