الحالة الإجهادية الحجمية

 الحالة الإجهادية الحجمية

نادراً ماتدرس في مقاومة المواد الإجهادات في الحالة الحجمية. وسنعرض في هذه الفقرة بعض العلاقات بشكلها المبسط، وعند الرغبة في التعمق أكثر من ذلك يمكننا العودة لنظرية المرونة.

من أجل الحالة الإجهادية الحجمية أو الفراغية فإنه تؤثر، في الحالة العامة ، إجهادات ناظمية و مماسية على جميع أوجه متوازي المستطيلات العنصري المقتطع dx , dy , dz حول نقطة ما بصورة كافية.

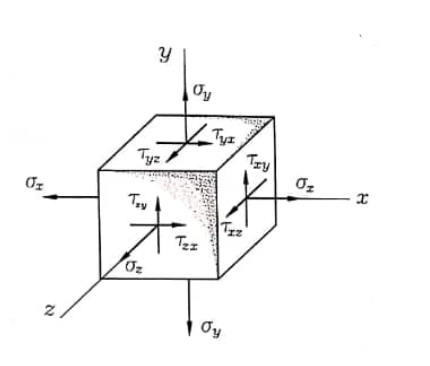
الشكل رقم (1)  

قانون ازدواج الإجهادات المماسية

إن مجموعة القوة المؤثرة على العنصرdx,dy,dz يجب أن تحقق شروط التوازن. بما أنه على الجوانب المتقابلة تظهر قوى متساوية ومتعاكسة فإن شروط التوازن الثلاثة محققة، ومجموع مساقط جميع القوى على المحاور z, y,x تساوي الصفر.

لكن هل مجموع عزوم جميع القوى بالنسبة للمحاور z,y,x يساوي الصفر؟

بتشكيل معادلات التوازن بسهولة يتبين أن عزم كل قوة ناظمية يتوازن بعزم القوة الناظمية المعاكسة المؤثرة على الجانب غير المرئي.

أما مجموع عزوم القوى المماسية بالنسبة للمحور x فيساوي صفراً عندما يكون عزم القوة Ꚍ_yz, dx, dz مساوياً لعزم القوة Ꚍ_xy, dx, dy أي أن:

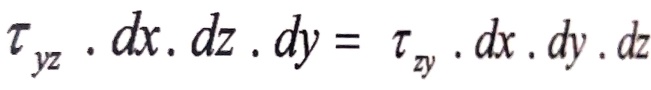      (1)

و بصورة مماثلة نكتب معادلتي التوازن الباقيتين، عندها ينتج:

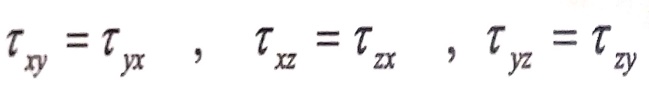   (2)

هذه العلاقة تسمى بقانون ازدواج الإجهادات المماسية في الحالة الحجمية، وتدل على أن الإجهادات المماسية على مستويين متعامدين تكون متساوية بالقيمة ومتجهة إما نحو الفصل المشترك بين المستويين أو مبتعدة عنها، أي تسعى لتدوير العنصر باتجاهات مختلفة.

الإجهادات في مستويات مائلة

نظرية:

إذا علمت المركبات الإجهادية الست σ_x , σ_y , σ_z , Ꚍ_xy , Ꚍ_yz , Ꚍ_zx ، في مقاطع ثلاثة متعامدة فيما بينها ، أمكننا تعيين الإجهادات في أي مقطع مار من تلك النقطة.

ولبرهان هذه النظرية سنقطع من الجسم المحمل، الشكل 1، وبجوار النقطة k عنصر حجمي بشكل موشور رباعي الوجوه، بحيث تتفق ثلاثة من وجوهه مع المستويات الإحداثية للجملة oxyz أما الوجه الرابع فيشكل مستوياً قاطعاً ذا وضعية عاملة ناظمه v، ونعين وضعية هذا الوجه بالتجيبات الموجهة :

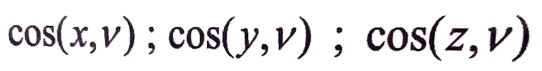
للناظم v على السطح المائل مع المحاور الإحداثية x,y,z  على الترتيب.

وللاختصار سوف نرمز للتجيبات الموجهة بـ:

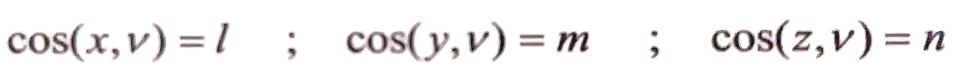   (3)

بتصغير رباعي الوجوه هذا فإنه سيتلاشى إلى النقطة k، وبالنهاية فإن جميع أوجهه ستمر من هذه النقطة، لذا يمكن اعتبار الإجهادات على جوانب هذا العنصر هي الإجهادات في النقطة المدروسة.

لنرمز لمساحة المثلث OBD بـ dAy ولمساحة المثلثdAx ولمساحة المثلث OBC بـ dAz وأخيرا لمساحة المثلث BCD بـ dA ومن الواضح أن:

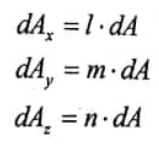    (4)