قاعدة سيمبسون III:
تدعى هذه الطريقة بطريقة أو قاعدة سيمبسون 5-8، تستخدم هذه الطريقة لحساب مساحة سطح محصور بين احداثيين رأسيين متتاليين، إذا كانت قيمة إحداثي رأسي مجاور لهما معلومة وبشرط أن تكون المسافة بين هذه الإحداثيات واحدة وتساوي طول قطاع التقسيم d.
لاستخراج معادلة سيمبسون III نأخذ قطاعاً من منحنٍ محدد بثلاثة إحداثيات رأسية تفصل بينها مسافات متساوية d كما في الشكل التالي، نستبدل هذا القطاع من المنحني بتابع منحنٍ من الدرجة الثانية كما في قاعدة سيمبسون I.
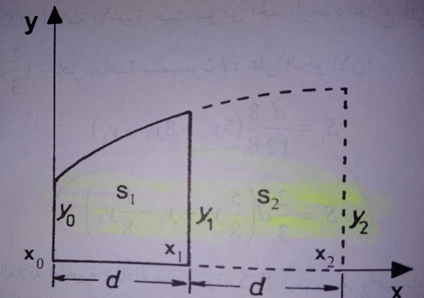
تحسب مساحة السطح بين الاإحداثيين y0 و y1 تقريباً كما يلي:

بالتالي تصبح مساحة السطح المدروس مساوية:

تدعى العلاقة الأخيرة بمعادلة سيمبسون 5-8 اليمينية وسميت بذلك لأن المساحة S1 تحسب بدلالة الإحداثي الرأسي y2 المجاور والواقع على يمين الرأسي الحدي y1 .
لحساب المساحة S2المبينة في الشكل السابق نتبع نفس الخطوات السابقة ولكن بعد جعل الإحداثي x2 مبدأ للإحداثيات اليسارية بحيث يتراوح مجال التكامل من 0 إلى d فنحصل على العلاقة التالية:









