المعادلات الأساسية في حساب الأسلاك اللينة
نقاط التثبيت لا تقع على منسوب واحد :
عند دراسة المعادلات الأساسية المستخدمة عند حساب الأسلاك اللينة في الحالة العامة عندما تكون نقاط تثبيت (المساند) الأسلاك غير واقعة على منسوب واحد . وفي هذه الحالة ، يتم غالبا تغيير الحمولة الموزعة ستاتيكيا والمؤثرة على طول السلك بحمولة مكافئة موزعة بانتظام q على طول الفتحة L ، أي على المسقط الأفقي للمسافة الكائنة بين نقاط التثبيت ، ووحدة قياسها تكون على شكل قوة على متر طولي (Kgf/m) :
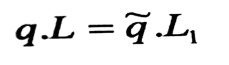
ومنه :
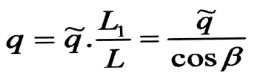
حيث :
L : طول الفتحة كمسقط للمسافة بين المساند .
L1 :المسافة الكائنة ما بين المساند .
نفترض أن السلك لين بشكل مثالي ويتحمل قوى شد ولا يتحمل أي نوع من الحالات الإجهادية الأخرى " انعطاف أو غيره " ، ونعتبر القوة الشادة في أي مقطع من مقاطع السلك مطبقة على المماس لخط السلك .
نختار مبدأ للإحداثيات في نقطة التثبيت اليسارية A ونعتبر المحاور الإحداثية y و x كما في الشكل رقم (1) .
القوة المؤثرة في السلك عند المساند A و B تساوي ردود الفعل TA و TB (قوى شادة مماسية) .
بتحليل ردود الفعل إلى مركبتين أفقية H و شاقولية R على المحاور الإحداثية وباستخدام معادلات التوازن الستاتيكية نجد :
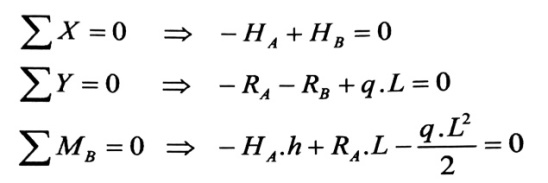
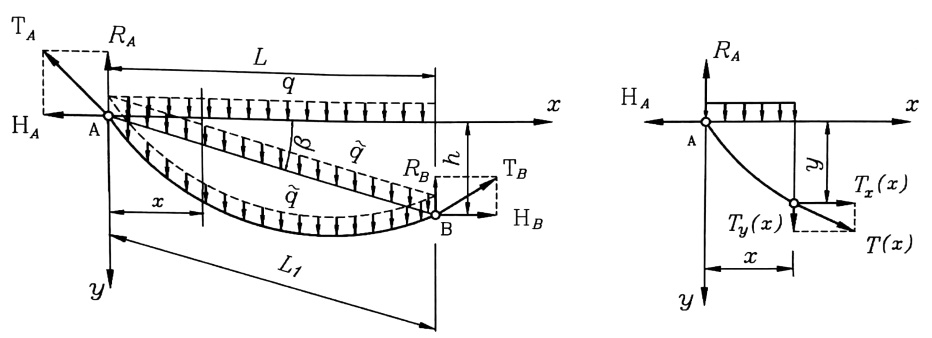
الشكل رقم (1)
وبحل المعادلات الثلاثة السابقة ، نجد :
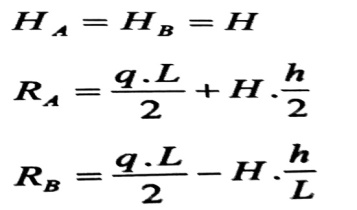(1,2,3)
وللحصول على قوة الشد T(x) المؤثرة في مقطع من السلك يقطع على مسافة x من مبدأ الإحداثيات نأخذ مقطعا " كما في الشكل رقم (1) " وندرس توازنه :
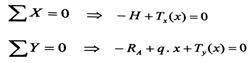
ومنه :
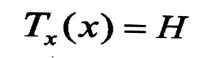(4)
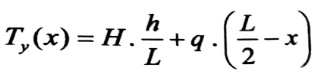(5)
حيث :
H : المركبة الأفقية لقوة الشد وهي ثابتة في كل المقاطع العرضية للسلك .
وبالتالي نجد أن محصلة القوة الشادة T(x) في أي مقطع للسلك تساوي :
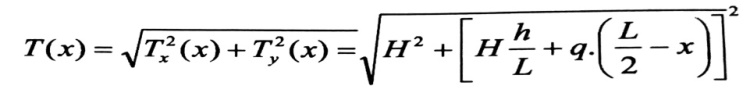(6)
ونحصل على قوة الشد العظمى عندما x = 0 :
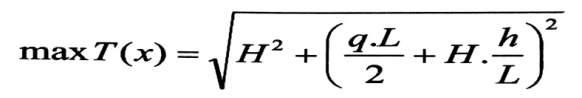(7)
ومن أجل الأسلاك ذات التدلي الصغير وطولها الفعلي لا يزيد عن (10%) من طول مسقطها الأفقي ، يكون الفرق بين قوة الشد العظمى T(x)max ومركبتها الأفقية H صغيرا ، ولهذا يكتفى في الحياة العملية عند حساب الأسلاك على المتانة أن نحققها وفق قيمة الشد H .
معادلة انحناء السلك :
ينحني السلك اللين تحت تأثير الحمولة الموزعة بانتظام q ، ولإيجاد معادلة هذا المنحني نجعل عزم الانعطاف عند مقطع على بعد x من مبدأ الإحداثيات مساويا الصفر :
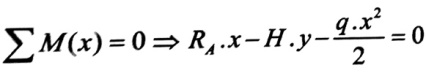
وبتعويض قيمة RA من المعادلة رقم (2) في المعادلة الأخيرة ، نجد :
Download eMufeed Android Application Now
